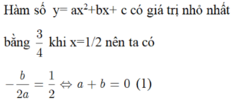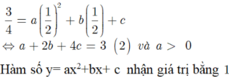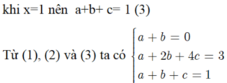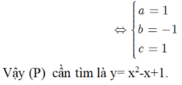Biết hs y = ax2 bx + c (a#0) đạt cực tiểu bằng 4 tại x = 2 và có đồ thị hàm số đi qua A(0;6). Tính P = abc
Những câu hỏi liên quan
Xác định parabol (P) ; y ax2+bx+ c biết: Hàm số y ax2+bx+ c có giá trị nhỏ nhất bằng 3/4 khi x1/2 và nhận giá trị bằng khi x1. A. y x2+ x+1. B. y- x2-x+1. C. y -x2-x-1. D. y x2-x+1
Đọc tiếp
Xác định parabol (P) ; y= ax2+bx+ c biết: Hàm số y= ax2+bx+ c có giá trị nhỏ nhất bằng 3/4 khi x=1/2 và nhận giá trị bằng khi x=1.
A. y= x2+ x+1.
B. y=- x2-x+1.
C. y= -x2-x-1.
D. y= x2-x+1
Xác định các hệ số a,b,c biết parabol y = ax2+bx+cax2+bx+c đi qua điểm A(2;3) và có đỉnh I ( 1;2 )
Tìm y=ax2+bx+c (p), biết (p) đi qua A(0;3),B(3;0),C(-1;1)
Xem chi tiết
Do (p) đi qua A(0;3), B(3;0) và C(-1;1) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}3=c\\9a+3b+c=0\\a+b+c=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}c=3\\3a+b=-1\\a+b=-4\end{matrix}\right.\\ \Leftrightarrow \left\{{}\begin{matrix}c=3\\a=\dfrac{3}{2}\\b=\dfrac{-11}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Đố. Đố em biết vì sao khi a 0 và phương trình
a
x
2
+
b
x
+
c
0
vô nghiệm thì
a
x
2
+
b
x
+
c
...
Đọc tiếp
Đố. Đố em biết vì sao khi a > 0 và phương trình a x 2 + b x + c = 0 vô nghiệm thì a x 2 + b x + c > 0 với mọi giá trị của x?
Ta có: a > 0 (gt), 
với mọi x, a, b ⇒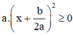 
Phương trình ax2 + bx + c = 0 vô nghiệm nên
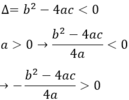
Vậy
a
x
2
+
b
x
+
c
= 
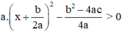với mọi x.
Đúng 0
Bình luận (0)
Đố. Đố em biết vì sao khi a > 0 và phương trình ax2 + bx + c = 0 vô nghiệm thì ax2 + bx + c > 0 với mọi giá trị của x?
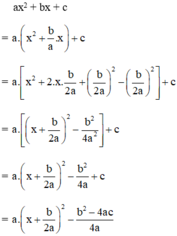
Ta có: a > 0 (gt),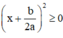 
với mọi x, a, b ⇒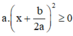 
Phương trình ax2 + bx + c = 0 vô nghiệm nên
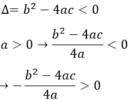
Vậy ax2 + bx + c =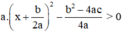 
với mọi x.
Đúng 0
Bình luận (0)
Xác định a, b, c biết parabol y = ax2 + bx + c Đi qua ba điểm A(0 ; -1), B(1 ; -1), C(-1 ; 1)
(P): y = ax2 + bx + c
Parabol đi qua A(0 ; –1) ⇒ –1 = a.02 + b.0 + c ⇒ c = –1.
Parabol đi qua B(1 ; –1) ⇒ –1 = a.12 + b.1 + c ⇒ a + b + c = –1.
Mà c = –1 ⇒ a + b = 0 (1)
Parabol đi qua C(–1; 1) ⇒ a.(–1)2 + b.(–1) + c = 1 ⇒ a – b + c = 1.
Mà c = –1 ⇒ a – b = 2 (2)
Từ (1) và (2) ⇒ a = 1; b = –1.
Vậy a = 1 ; b = –1 ; c = –1.
Đúng 0
Bình luận (0)
Xác định a, b, c biết parabol y = ax2 + bx + c đi qua điểm A(8 ; 0) và có đỉnh là I(6 ; -12).
+ Parabol y = ax2 + bx + c đi qua điểm A (8; 0)
⇒ 0 = a.82 + b.8 + c ⇒ 64a + 8b + c = 0 (1).
+ Parabol y = ax2 + bx + c có đỉnh là I (6 ; –12) suy ra:
–b/2a = 6 ⇒ b = –12a (2).
–Δ/4a = –12 ⇒ Δ = 48a ⇒ b2 – 4ac = 48a (3) .
Thay (2) vào (1) ta có: 64a – 96a + c = 0 ⇒ c = 32a.
Thay b = –12a và c = 32a vào (3) ta được:
(–12a)2 – 4a.32a = 48a
⇒ 144a2 – 128a2 = 48a
⇒ 16a2 = 48a
⇒ a = 3 (vì a ≠ 0).
Từ a = 3 ⇒ b = –36 và c = 96.
Vậy a = 3; b = –36 và c = 96.
Đúng 0
Bình luận (0)
Cho parabol (P) ; y= ax2+bx+ c biết: (P) đi qua A(2;3) có đỉnh I( 1;2) . Hỏi a+ b+c bằng bao nhiêu.
A. -2
B.-1
C. 0
D.2
Xác định a, b, c biết parabol y = ax2 + bx + c Có đỉnh I(1 ; 4) và đi qua điểm D(3 ; 0)
(P) : y = ax2 + bx + c
Parabol có đỉnh I(1 ; 4) ⇒ –b/2a = 1 ⇒ b = –2a ⇒ 2a + b = 0.
Parabol đi qua I(1; 4) ⇒ 4 = a.12 + b . 1 + c ⇒ a + b + c = 4.
Paraol đi qua D(3; 0) ⇒ 0 = a.32 + b.3 + c ⇒ 9a + 3b + c = 0.
Giải hệ phương trình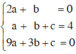 
ta được : a = –1 ; b = 2 ; c = 3.
Vậy a = –1 ; b = 2 ; c = 3.
Đúng 0
Bình luận (1)
Biết parabol (P) y = ax2 + bx + c có đỉnh nằm trên trục hoành và đi qua 2 điểm A(0;1) , B(2;1).
Tổng a + b + c là:
\(ĐK:a\ne0\)
\(A\left(0;1\right)\in\left(P\right)\Leftrightarrow c=1\)
(P) có đỉnh trên trục hoành \(\Leftrightarrow\Delta=b^2-4ac=0\Leftrightarrow b^2=4ac=4a\Leftrightarrow a=\dfrac{b^2}{4}\)
\(B\left(2;1\right)\in\left(P\right)\Leftrightarrow4a+2b+c=1\\ \Leftrightarrow b^2+2b=0\\ \Leftrightarrow\left[{}\begin{matrix}b=0\Leftrightarrow a=0\left(ktm\right)\\b=-2\Leftrightarrow a=1\left(tm\right)\end{matrix}\right.\)
Vậy \(a+b+c=1-2+1=0\)
Đúng 2
Bình luận (0)