Cho tam giác ABC vuông cân tại A. Trên tia đối của tia BC lấy điểm D sao cho BD=BA.Tính góc ADB

Những câu hỏi liên quan
Cho tam giác ABC vuông cân tại A.Trên tia đối của tia BC lấy điểm D sao cho BD=BA.Tính số đo góc ADB
Các bạn ơi giúp mink nhé ngày mai mink nộp bài rồi
Cho tam giác ABC vuông cân tại A. Trên tia đối của tia BC lấy điểm D sao cho BD = BA. Tính số đo góc ADB
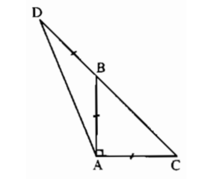
+) Do tam giác ABC vuông cân tại A nên:
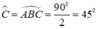
+) Tam giác ABD có AB = BD nên tam giác ABD cân tại B.
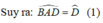
+) Tam giác ABD có góc ABC là góc ngoài tam giác tại đỉnh B nên:
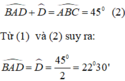
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A. Trên tia đối của tia BC lấy điểm D sao cho BD = BA. Tính số đo góc ADB ?
Ta có hình vẽ:
Ta có: tam giác ABC vuông cân tại A
=> góc ABC = 450
Ta có: góc ABC + góc ABD = 1800
hay 450 + góc ABD = 1800
=> góc ABD = 1800 - 450 = 1350
Ta có: góc DAB + góc ABD + góc ADB = 1800
hay góc DAB + góc ADB + 1350 = 1800
=> góc DAB + góc ADB = 450
Ta có: BD = BA => tam giác BDA cân
=> góc DAB = góc ADB = 450 /2 = 2205'
Đúng 0
Bình luận (0)
ΔABC vuông cân ở A (giả thiết) => ∠ABC = 45°.
ΔABD có BA = BD (giả thiết) => ΔABD cân ở B.
Mà ∠ABD, ∠ABC kề bù.
=> ∠ADB = (180° - ∠ABD)/2 = ∠ABC/2 = 45°/2 = 22,5°.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A. Trên tia đối của tia BC lấy điểm D sao cho BD = BA. Tính số đo góc ADB
+ Ta có: ˆABC+ˆABD=ˆACE+ˆBCA=180oABC^+ABD^=ACE^+BCA^=180o (Vì kề bù). Mà ˆABC=ˆBCA⟹ˆABD=ˆACEABC^=BCA^⟹ABD^=ACE^
+ Ta có: AB=AC (△ABC△ABC cân ở A ). Mà AB=BD;AC=CE⟹AB=BD=AC=CEAB=BD;AC=CE⟹AB=BD=AC=CE
+ Xét: △ABD△ABD và △ACE△ACE ta có:
AB=AC (△ABC△ABC cân ở A )
BD=CE (CM trên)
ˆABD=ˆACEABD^=ACE^ (CM trên)
⟹△ABD=△ACE⟹△ABD=△ACE (cgc)
⟹AD=AE⟹AD=AE (2 cạnh tương ứng) ⟹△ADE⟹△ADE cân ở A
+ Ta có BD=CE; BQ=QC⟹DQ=EQBD=CE; BQ=QC⟹DQ=EQ
+ △ADE△ADE cân ở A có AQ là đường trung tuyến đồng thời là tia phân giác ˆDAEDAE^ (1)
+ Ta có: DB=AB ⟹△BAD⟹△BAD cân ở B có trung tuyến BM đồng thời là đường cao. ⟹BM⊥AD⟹BM⊥AD
+ Ta có: CE=AC ⟹△ACE⟹△ACE cân ở C có trung tuyến CN đồng thời là đường cao. ⟹CN⊥AE⟹CN⊥AE
+ Ta có: AD=AE⟹AD2=AE2⟹AM=ANAD=AE⟹AD2=AE2⟹AM=AN
+ Xét △AMO△AMO và △ANO△ANO ta có:
ˆAMO=ˆANO=90oAMO^=ANO^=90o
AO chung
AM=AN (CM trên)
⟹△AMO=△ANO⟹△AMO=△ANO (ch-cgv)
⟹ˆAOM=ˆAON⟹AOM^=AON^ (2 góc tương ứng)
⟹AO⟹AO là tia phân giác góc DAE (2)
+ Từ (1); (2) ta có 3 điểm A;O;Q thẳng hàng
Vậy 3 đường thẳng AQ; BM;CN đồng quy tại O
Đúng 0
Bình luận (0)
hinh tu ve nha
XÉT TAM GIÁC ABC VUÔNG CÂN Ở A CÓ
A=900 SUY RA GÓC ABC=ACB=900
GÓC ABC=GÓC ACB( ĐN TAM GIÁC CÂN)
SUY RA GÓC ABC= GÓC ACB=900:2=450
CÓ BD=BA
SUY RA TAM GIÁC DBA CÂN TẠI A ( DN TAM GIÁC CÂN)
CÓ GÓC ABC VÀ GÓC ABD LÀ 2 GÓC KỀ BÙ
SUY RA ABC+ABD=1800
THAY SỐ ĐƯỢC
450+ABD=1800
ABD=1800-450
ABD=1350
SUY RA GÓC D = GÓC BAD( ĐN TAM GIÁC CÂN)
SUY RA GÓC ADB= GÓC BAD=(1800-1350):2=22,50
K CHO MÌNH NHA
Đúng 0
Bình luận (0)
Câu hỏi : Cho tam giác ABC vuông cân tại A .Trên tia đối của tia BC lấy điểm D sao cho BD=AB.Tính số đo góc ADB.
Vì tam giác ABC vuông cân tại A => ^B=^C=45o
^ABC+^ABD=180o(2 góc kề bù). Mà ^ABC=45o(cmt)=>^ABD=135o
Xét tam giác BAD, có BA=BD(gt)=> Tam giác BAD cân tại B
=> ^BAD=^BDA= \(\frac{180^o-\widehat{DBA}}{2}\)
=\(\frac{180^o-135^o}{2}\)
=22.5o
\(\Delta ABC\)là tam giác vuông cân tại \(gócA\)
=> góc CBA = Góc BCA = \(\frac{90^o}{2}=45^o\)
Mà góc DBA + góc CBA = \(180^o\)
=> góc DBA = \(180^o-45^o=135^o\)
\(\Delta DBA\)là tam giác cân tại B ( DB=BA)
=> \(gócBDA=gócBAD=\frac{180^o-gócDBA}{2}=\frac{45^o}{2}\approx22^o30^'\)
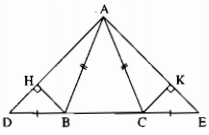
cho tam giác abc cân tại a kẻ phân giác ad (d thuộc bc) trên tia đối tia bc lấy điểm d sao cho bd=ba đường vuông góc với bc tại d cắt ac tại e chứng minh rằng
a be là đường trung trực của ad
b tia ad là tia ad là tia pg của góc hac
c hd<dc d kẻ cf vuông góc với be tại f cmr ba đường thẳng ab,de,cf đòng quy
Xem chi tiết
a be là đường trung trực của ad
b tia ad là tia ad là tia pg của góc hac
c hd<dc d kẻ cf vuông góc với be tại f cmr ba đường thẳng ab,de,cf đòng quy
cho tam giác abc cân tại a,trên tia đối của tia bc lấy điểm d,trên tia đối của tia cb lấy điểm e sao cho bd=ce.kẻ bh vuông góc với ad tại h,kẻ ck vuông góc với ae tại k.chứng minh tam giác bhd=tam giác cke
cho tam giác ABC vuông tại A , AH vuông góc với BC . Trên tia đối của tia AH lấy D sao cho AD=BC , trên tia đối của tia CA lấy E sao cho CE=AB
a chứng mih tam giác ADB = tam giác CBE
b chứng minh tam giác EDB VUÔNG CÂN
c Vẽ AI vuông góc với BD . AI cắt DE tại K . Chứng minh KC vuông góc vs BE
Bài 1: Cho tam giác ABC đều. Trên tia đối tia BC lấy điểm D, trên tia đối tia CB lấy điểm E sao cho BDCEBCa) C/m: tam giác ACE cânb) Tính góc DAEBài 2: Cho tam giác ABC cân tại A. Trên tia đối tia AC lấy điểm D sao cho AD AC. C/m tam giác BCD vuôngBài 3: Cho tam giác ABC cân tại A có góc A 40 độ. Lấy điểm D khác phía B so với AC thoả mãn góc CAD60 độ, góc ACD80 độ. C/m BD vuông góc AC
Đọc tiếp
Bài 1: Cho tam giác ABC đều. Trên tia đối tia BC lấy điểm D, trên tia đối tia CB lấy điểm E sao cho BD=CE=BC
a) C/m: tam giác ACE cân
b) Tính góc DAE
Bài 2: Cho tam giác ABC cân tại A. Trên tia đối tia AC lấy điểm D sao cho AD = AC. C/m tam giác BCD vuông
Bài 3: Cho tam giác ABC cân tại A có góc A= 40 độ. Lấy điểm D khác phía B so với AC thoả mãn góc CAD=60 độ, góc ACD=80 độ. C/m BD vuông góc AC