cho a,b tùy ý CM (a^2+b^2)/2 >= ab
cho a>0 CM a+1/a >=2
c CM x^2+y^2+z^2+3>=2
Những câu hỏi liên quan
Giải giup giùm em em cần gấp ạ nghĩ mãi mà vẫn không ra
a)CM: 3(a^2+b^2+c^2)>=(a+b+c)^2 với a,b,c bất kỳ
b) Cho x>0,y>0,z>0 và x+y+z=1.CM:(x+1/x)^2+(y+1/y)^2+(z+1/z)^2>=100/3
Xác định giá trị nhỏ nhất của các biểu thức:
a)A=4x^2+9/x với x thay đổi, x>0
b) B= x^2+2y^2+3x-y+6 với x,y thay đổi
CM bất đẳng thức sau: a^2b^2+b^2c^2+c^2a^2>= abc(a+b+c) (a,b,c bất kỳ)
cho x,y,z thuộc khoảng 0 đến 1 thỏa mãn x+y+z=0 cm a^2+b^2+c^2<=1+a^2b+b^2c+c^2a
Bài 1:
a) x3+y3+z3 = xy+yz+xz. Cm: x=y=z.
b) (x+y+z)3 = 3(xy+yz+xz). Cm: x=y=z.
Bài 2:
a) Cho a+b+c=0. Cm: (a2+b2+c2)2 = 2(a4+b4+c4).
b) Cho (a2+b2)(x2+y2) = (ax+by)2. Cm: ay = bx (x,y khác 0)
a,cho (a/b+c)+(b/c+a)+(c/a+b)=1.cm (a2/b+c)+(b2/c+a)+(c2/a+b)=0
b,cho (x/a)+(y/b)+(z/c)=1va(a/x)+(b/y)+(c/z)=0
cm(x2/a2)+(y2/b2)+(z2/c2)=1
a, \(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}=1\)
\(\Leftrightarrow\left(a+b+c\right)\left(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\right)=a+b+c\)
\(\Leftrightarrow\frac{a\left(a+b+c\right)}{b+c}+\frac{b\left(a+b+c\right)}{c+a}+\frac{c\left(a+b+c\right)}{a+b}=a+b+c\)
\(\Leftrightarrow\frac{a^2+a\left(b+c\right)}{b+c}+\frac{b^2+b\left(a+c\right)}{c+a}+\frac{c^2+c\left(a+b\right)}{a+b}=a+b+c\)
\(\Leftrightarrow\frac{a^2}{b+c}+a+\frac{b^2}{c+a}+b+\frac{c^2}{a+b}+c=a+b+c\)
\(\Leftrightarrow\frac{a^2}{b+c}+\frac{b^2}{c+a}+\frac{c^2}{a+b}=0\) (đpcm)
b, Từ \(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}=0\Rightarrow\frac{ayz+bxz+cxy}{xyz}=0\) hay ayz+bxz+cxy=0
Từ \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\Rightarrow\left(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\right)^2=1\)
\(\Rightarrow\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}+2\left(\frac{xy}{ab}+\frac{yz}{bc}+\frac{zx}{ca}\right)=1\)
\(\Rightarrow\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}+2\cdot\frac{cxy+ayz+bzx}{abc}=1\)
Mà ayz+bxz+cxy=1
=>\(\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1\) (đpcm)
Đúng 0
Bình luận (0)
1. a,b,c0 và a+b+c2017CM:Sigmadfrac{2017a-a^2}{bc}gesqrt{2}left(Sigmasqrt{dfrac{2017-a}{a}}right)2. cho x,y,z tm: x^2+y^2+z^23CM:8left(2-xright)left(2-yright)left(2-zright)geleft(x+yzright)left(y+zxright)left(z+xyright)3. a,b,c0 và a^2+b^2+c^2ge6CM:Sigmadfrac{1}{1+ab}gedfrac{3}{2}
Đọc tiếp
1. a,b,c>0 và a+b+c=2017
\(CM:\Sigma\dfrac{2017a-a^2}{bc}\ge\sqrt{2}\left(\Sigma\sqrt{\dfrac{2017-a}{a}}\right)\)
2. cho x,y,z tm: \(x^2+y^2+z^2=3\)
\(CM:8\left(2-x\right)\left(2-y\right)\left(2-z\right)\ge\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)\)
3. a,b,c>0 và \(a^2+b^2+c^2\ge6\)
\(CM:\Sigma\dfrac{1}{1+ab}\ge\dfrac{3}{2}\)
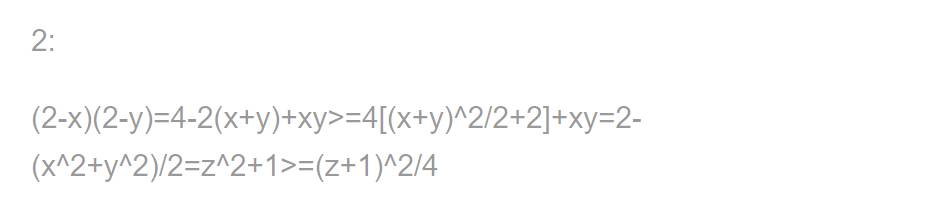
Tương tự, ta được:
\(\left(2-y\right)\left(2-z\right)>=\dfrac{\left(x+1\right)^2}{4}\)
và \(\left(2-z\right)\left(2-x\right)>=\left(\dfrac{y+1}{2}\right)^2\)
=>8(2-x)(2-y)(2-z)>=(x+1)(y+1)(z+1)
(x+yz)(y+zx)<=(x+y+yz+xz)^2/4=(x+y)^2*(z+1)^2/4<=(x^2+y^2)(z+1)^2/4
Tương tự, ta cũng co:
\(\left(y+xz\right)\left(z+y\right)< =\dfrac{\left(y^2+z^2\right)\left(x+1\right)^2}{2}\)
và \(\left(z+xy\right)\left(x+yz\right)< =\dfrac{\left(z^2+x^2\right)\left(y+1\right)^2}{2}\)
Do đó, ta được:
\(\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)< =\left(x+1\right)\left(y+1\right)\left(z+1\right)\)
=>ĐPCM
Đúng 0
Bình luận (0)
cho a b c và x y z thỏa mãn a+b+c=1(1) a^2+b^2+c^2=1(2), x/a=y/b=z/c(3). Cm xy+yz+xz=0
1/ Cho a. b. c0 và a+b+c 1CM: Pabcleft(a+bright)left(b+cright)left(c+aright) frac{1}{64}2/ Cho x, y, z 0 thỏa x^3+y^3+z^31CM: frac{x^2}{sqrt{1-x^2}}+frac{y^2}{sqrt{1-y^2}}+frac{z^2}{sqrt{1-z^2}}23/ Cho x,y 0 vàx+yle1CM: frac{1}{x^2+xy}+frac{1}{y^2+xy}ge44/ Cho a, b, c là 3 cạnh tam giác a) CM: a^2left(1+b^2right)+b^2left(1+c^2right)+c^2left(1+a^2right)ge6abcb) CM: a^3+b^3+c^3ge3abc5/ Cho tam giác ABC có các cạnh age bge cCM: frac{b}{a}+frac{c}{b}+frac{a}{c}gefrac{a}{b}+frac{b}{c}+frac{c}{a}6/ Ch...
Đọc tiếp
1/ Cho a. b. c>0 và a+b+c= 1
CM: \(P=abc\left(a+b\right)\left(b+c\right)\left(c+a\right)< \frac{1}{64}\)
2/ Cho x, y, z> 0 thỏa \(x^3+y^3+z^3=1\)
CM: \(\frac{x^2}{\sqrt{1-x^2}}+\frac{y^2}{\sqrt{1-y^2}}+\frac{z^2}{\sqrt{1-z^2}}>2\)
3/ Cho x,y >0 và\(x+y\le1\)
CM: \(\frac{1}{x^2+xy}+\frac{1}{y^2+xy}\ge4\)
4/ Cho a, b, c là 3 cạnh tam giác
a) CM: \(a^2\left(1+b^2\right)+b^2\left(1+c^2\right)+c^2\left(1+a^2\right)\ge6abc\)
b) CM: \(a^3+b^3+c^3\ge3abc\)
5/ Cho tam giác ABC có các cạnh \(a\ge b\ge c\)
CM: \(\frac{b}{a}+\frac{c}{b}+\frac{a}{c}\ge\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\)
6/ Cho \(x,y\ge1\)
CM: \(\frac{1}{1+x^2}+\frac{1}{1+y^2}\ge\frac{2}{1+xy}\)
1. Cho a+b+c=a^2+b^2+c^2=1 và a/x=b/y=c/z
Cm: xy+yz+zx=0
2.Cho x/a+y/b+z/c=1 và a/x^2+b/y^2+c/z^2=0
Tính: A=x^2/a^2+y^2/b^2+z^2/c^2
3.Tìm a,b biết:(a-1)^2+(b-1)^2=10a+b
và 0<a<10; -1<b<10
Ta có: a+b+c=1 <=>(a+b+c)2 = 1 <=> ab+bc+ca=0 (1)
Theo dãy tỉ số bằng nhau ta có:
xa=yb=zc=x+y+za+b+c=x+y+z1=x+y+zxa=yb=zc=x+y+za+b+c=x+y+z1=x+y+z
<=> x = a(x+y+z) ; y = b(x+y+z) ; z = c(x+y+z)
=> xy+yz+zx= ab(x+y+z)2+bc(x+y+z)2+ca(x + y + z)2
<=> xy+yz+zx =(ab+bc+ca)(x+y+z)2 (2)
từ (1) và (2) => xy + yz + zx = 0
Bai1 : Tim max voi x thuoc [1;3]
F(x) = (x-1)(3-x)
G(x)=(2x-1)(3-x)
Bai2: cho a,b>0 thoa man 4/a+1/b=1
Tim min p=a+b
Bai3: cm Voi moi a>0 ta co a^2(1-2a)<=1/27
Bai4: cho a,b,c >0 tm ab+bc+ca=3
Cm a^3+b^3+c^3>=3
Bai5: x,y,z>0 tm xyz=1
Cm x^2\1+y +y^2\1+z + z^2\1+x