Cho hình thang ABCD có AB song song với CD và AB<CD. Gọi O là giao điểm 2 đường chéo AC và BD.
a) Chứng minh rằng DC-AB<AD+BC
b)Cho SAOB=\(a^2\) SDOC=\(b^2\). Chứng minh SABCD=\(\left(a+b\right)^2\)
Cho hình thang ABCD (AB song song với CD, AB<CD). Đường thẳng song song với AB cắt các cạnh AD, BC lần lượt tại M và N và chia hình thang ABCD thành 2 hình có diện tích bằng nhau. CMR: \(MN^2=\dfrac{AB^2+DC^2}{2}\)
Cho hình thang cân ABCD (AB song song với CD) có AB = 7cm, BC = CD= 13cm. Kẻ các đường cao AK và BH
a) Chứng minh rằng CH=DK và AB = HK
b) Tính độ dài BH và diện tích hình thang ABCD
a: Xét ΔAKD vuông tại K và ΔBHC vuông tại H có
AD=BC
góc D=góc C
=>ΔAKD=ΔBHC
=>CH=DK
Xét tứ giác ABHK có
AB//HK
AK//HB
=>ABHK là hình bình hành
=>AB=HK
b: KH=AB=7cm
=>DK+HC=13-7=6cm
=>DK=HC=6/2=3cm
\(BH=\sqrt{13^2-3^2}=\sqrt{160}=4\sqrt{10}\left(cm\right)\)
\(S_{ABCD}=\dfrac{1}{2}\cdot BH\cdot\left(AB+CD\right)\)
\(=\dfrac{1}{2}\cdot4\sqrt{10}\left(7+13\right)=40\sqrt{10}\left(cm^2\right)\)
cho hình thang abcd có ab song song cd m thuộc hình thang vẽ các hình bình hành abcd e f chứng minh rằng ef song song cd ab = ab + cd
Bài 1: Cho hình thang ABCD ( có AB// CD). Gọi E là trung điểm của AD. Kẻ đường thẳng qua E song song với AB và cắt BC tại F.
a) Chứng minh F là trung điểm của BC.
b) Cho AB = 4; CD =12. Tính EF.
Bài 2: Cho hình thang ABCD (có AB // CD; AB < CD). Gọi E, F, G lần lượt là trung điểm của AD, AC, BD.
a) Chứng minh E, F, G thẳng hàng.
b) Chứng minh EF = (CD-AB)/2.
Bài 1: Cho hình thang ABCD ( có AB// CD). Gọi E là trung điểm của AD. Kẻ đường thẳng qua E song song với AB và cắt BC tại F.
a) Chứng minh F là trung điểm của BC.
b) Cho AB = 4; CD =12. Tính EF.
Bài 2: Cho hình thang ABCD (có AB // CD; AB < CD). Gọi E, F, G lần lượt là trung điểm của AD, AC, BD.
a) Chứng minh E, F, G thẳng hàng.
b) Chứng minh EF = (CD-AB)/2.
Cho hình thang ABCD có AB song song với CD. Cho AB=2a và CD= a. Gọi O là trung điểm của AD. Khi đó:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hình thang cân ABCD có AB song song với CD và ab<cd
biết ad=bc
a) cm ab=bc
b) cm db là phân giác adc
Đề bài phải sửa thành "biết AD=AB" mới làm được
a/
ABCD là hình thàng cân => AD=BC
Mà AD=AB (gt)
=> AD=BC
b/
ABCD là hình thang cân
\(\Rightarrow\widehat{BAD}=\widehat{ABC}\)
\(\widehat{BCD}+\widehat{ABC}=180^o\) (Hai góc trong cùng phía)
\(\Rightarrow\widehat{BCD}+\widehat{BAD}=180^o\)
=> ABCD là tứ giác nội tiếp (Tứ giác có tổng 2 góc đối bù nhau là tứ giác nt)
Ta có
Cung AB và cung BC có hai dây trương cung bằng nhau
AB=BC (cmt) => sđ cung AB = sđ cung BC (1)
\(sđ\widehat{ADB}=\dfrac{1}{2}sđcungAB\) (góc nội tiếp) (2)
\(sđ\widehat{CDB}=\dfrac{1}{2}sđcungBC\) (góc nội tiếp) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{ADB}=\widehat{CDB}\) => DB là phân giác của \(\widehat{ADC}\)
Cho hình thang ABCD (AB song song với CD, AB>CD) có diện tích bằng 1 và \(BD\ge AC\). CHứng minh: \(BD\ge\sqrt{2}\)
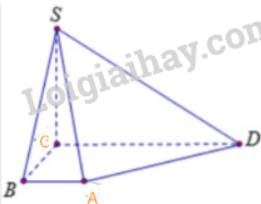
Vẽ hình biểu diễn của hình chóp S.ABCD có đáy ABCD là hình thang, AB song song với CD và AB = 2cm, CD = 6cm.
Tham khảo:
Hình chóp S.ABCD có các mặt bên là hình tam giác nên hình biểu diễn của nó cũng các mặt bên là hình tam giác
Hình thang ABCD có AB//CD và AB=2cm, CD=6cm nên hình biểu diễn của ABCD là một hình thang có đáy CD gấp ba đáy BC
Từ đó, ta vẽ được hình biểu diễn của S.ABCD.
Bài 1. Cho hình thang cân ABCD (AB//CD) có D̂ = 600, CD = 49 cm, AB = 15 cm. Qua B vẽ đường thẳng song song với AD cắt CD tại E
a) Chứng minh rằng BCE là tam giác đều.
b) Tính EC và chu vi hình thang ABCD.
Xét hình thang cân ABCD có
Góc D = 60 độ
=> Góc C=60 độ ( định lí hình thang cân)
Xét tamm giác BEC
Có góc C=60 độ
=> Tam giác BEC đều ( định lí tam giác đều)