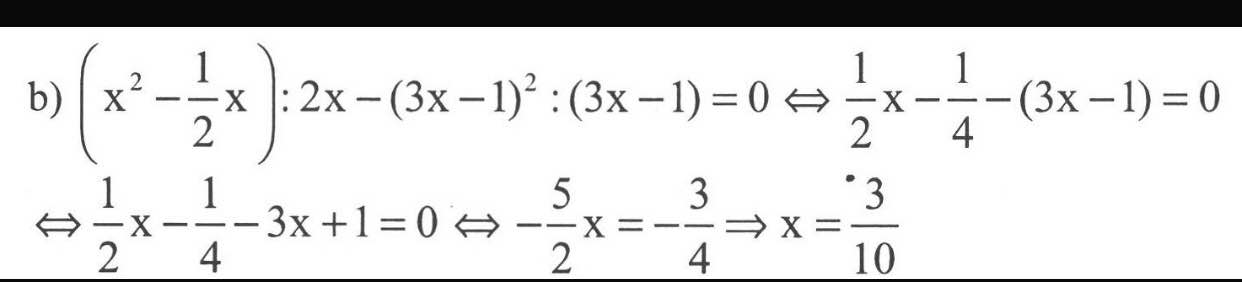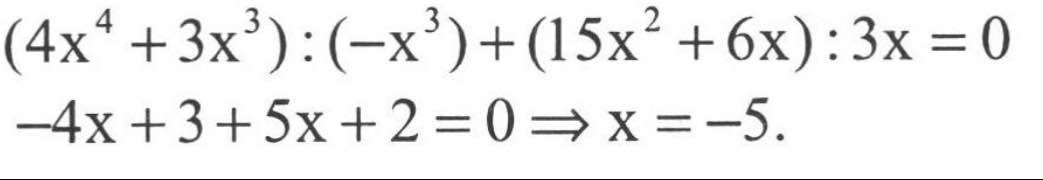6x (3x + 1)-216 (3x 1 ) = 0

Những câu hỏi liên quan
Bài 3: Rút gọn biểu thức:
a) (6x+1)2+(6x-1)2-2(1+6x)(6x-1); b) 3(22+1)(24+1)(28+1)(216+1); c) x(2x2-3)-x2(5x+1)+x2; d) 3x(x-2)-5x(1-x)-8(x2-3)
a)\(4x+3x=217\)
b)\(9x-3x=216\)
c)\(6x-3x+23=230\)
d)\(5x+3x+x=72\)
giúp mk với mn ơi😢
a) 4x + 3x = 217
x( 4 + 3 ) = 217
7x = 217
x = 217 : 7 = 31
Vậy x = 31
b) 9x - 3x = 216
( 9 -3)x = 216
6x = 216
x = 216:6 = 36
Vậy x = 36
c) 6x - 3x + 23 = 230
( 6 - 3 )x = 230 - 23
3x = 207
x = 207 : 3 = 69
Vậy x = 69
d) 5x + 3x + x = 72
5x + 3x + 1x = 72
( 5 + 3 + 1 )x = 72
9x = 72
x = 72 : 9 = 8
Vậy x = 8
Chúc bạn học tốt nhé
Đúng 4
Bình luận (0)
a) \(4x+3x=217\)
\(\Rightarrow x\cdot\left(3+4\right)=217\)
\(\Rightarrow7x=217\)
\(\Rightarrow x=\dfrac{217}{7}\)
\(\Rightarrow x=31\)
b) \(9x-3x=216\)
\(\Rightarrow x\cdot\left(9-3\right)=216\)
\(\Rightarrow6x=216\)
\(\Rightarrow x=\dfrac{216}{6}\)
\(\Rightarrow x=36\)
c) \(6x-3x+23=230\)
\(\Rightarrow x\cdot\left(6-3\right)=230-23\)
\(\Rightarrow3x=207\)
\(\Rightarrow x=\dfrac{207}{3}\)
\(\Rightarrow x=69\)
d) \(5x+3x+x=72\)
\(\Rightarrow x\cdot\left(5+3+1\right)=72\)
\(\Rightarrow9x=72\)
\(\Rightarrow x=\dfrac{72}{9}\)
\(\Rightarrow x=8\)
Đúng 3
Bình luận (0)
Xem thêm câu trả lời
GIẢI CÁC PHƯƠNG TRÌNH SAU:
2x3+6x2+6x+1=0
X^3-3X^2+3X-3=0
2X^3+6X^2+6X+1=0
3X^3+18X^2+36X+23=0
(x^2-1/2x):2x-(3x-1)^2.(3x-1)=0
(4x^4 + 3x3) : (-x^3) + (15x2 + 6x) : 3x =0
Ta có: \(\dfrac{4x^4+3x^3}{-x^3}+\dfrac{15x^2+6x}{3x}=0\)
\(\Leftrightarrow-4x-3+5x+2=0\)
\(\Leftrightarrow x-1=0\)
hay x=1
Đúng 0
Bình luận (0)
A=x+6x^2+7x^2-6x+1
A=(x^2)^2+2x^2.3x+9x^2-1x^2-6x+7
A=(x^2+3x)^2-2.(x^2+3x).1+1
A=(x^2+3x)^2>=0 với mọi x khi x^2=3x-1=0
|5x+8|=0
|1-3x|=1
|3x+2|=-3
|x-1|=3x+5
|2x-3|=3x-5
|1-6x|=3x+1
giúp em với
1
\(\left|5x+8\right|=0\\ 5x+8=0\\ 5x=8\\ x=\dfrac{8}{5}\\ x=1.6\)
2
\(\left|1-3x\right|=1\\ 1-3x=1\\ \Rightarrow\left\{{}\begin{matrix}1-3x=1\Leftrightarrow3x=0\Leftrightarrow x=0\\1-3x=\left(-1\right)\Leftrightarrow3x=-2\Leftrightarrow x=\dfrac{-2}{3}\end{matrix}\right.\)
3
\(\left|3x+2\right|=-3\Rightarrow\varnothing\)
phương trình vô nghiệm vì giá trị tuyệt đối của mọi số điều không âm
4
\(|x-1|=3x+5\) (1)
Ta có \(|x-1|= x-1 \) khi \(x-1\ge0\Rightarrow x\ge1\)
\(\left|x-1\right|=-\left(x-1\right)=1-x\) khi \(x-1< 0\Rightarrow x< 1\)
Với \(x\ge1\) phương trình (1)
\(x-1=3x+5\\ \Leftrightarrow x-3x=5+1\\ \Leftrightarrow-2x=6\\ \Leftrightarrow x=\dfrac{-6}{2}=-3\)
x= -3 không thỏa mãn điều kiện
Với \(x< 1\) phương trình (1)
\(1-x=3x+5\\ \Leftrightarrow-x-3x=5-1\\ \Leftrightarrow-4x=4\\ \Leftrightarrow-4x\cdot\dfrac{-1}{4}=4\cdot\dfrac{-1}{4}\\ \Leftrightarrow x=-1\)
x=-1 thỏa mãn điều kiện
:v cậu đăng ít thôi nhé pai pai
này mình chưa học đâu cớ tuần sau mới học ấy nhưng mà mình coi dạng rồi làm cho cậu nè ;-;
Đúng 0
Bình luận (0)
Giải các phương trình sau
1. x^4+3x^3-2x^2-6x+4=0
2. x^4-3x^3-6x^2+3x+1=0
x4−3x3−2x2+6x+4=0x4−3x3−2x2+6x+4=0
⇔x4−2x3−2x2−x3+2x2+2x−2x2+4x+4=0⇔x4−2x3−2x2−x3+2x2+2x−2x2+4x+4=0
⇔x2(x2−2x−2)−x(x2−2x−2)−2(x2−2x−2)=0⇔x2(x2−2x−2)−x(x2−2x−2)−2(x2−2x−2)=0
⇔(x2−x−2)(x2−2x−2)=0⇔(x2−x−2)(x2−2x−2)=0
⇔(x+1)(x−2)(x−1−√3)(x−1+√3)=0⇔(x+1)(x−2)(x−1−3)(x−1+3)=0
⇔⎡⎢ ⎢ ⎢ ⎢⎣x=−1x=2x=1+√3x=1−√3
tl
x4−3x3−2x2+6x+4=0x4−3x3−2x2+6x+4=0
⇔x4−2x3−2x2−x3+2x2+2x−2x2+4x+4=0⇔x4−2x3−2x2−x3+2x2+2x−2x2+4x+4=0
⇔x2(x2−2x−2)−x(x2−2x−2)−2(x2−2x−2)=0⇔x2(x2−2x−2)−x(x2−2x−2)−2(x2−2x−2)=0
⇔(x2−x−2)(x2−2x−2)=0⇔(x2−x−2)(x2−2x−2)=0
⇔(x+1)(x−2)(x−1−√3)(x−1+√3)=0⇔(x+1)(x−2)(x−1−3)(x−1+3)=0
⇔⎡⎢ ⎢ ⎢ ⎢⎣x=−1x=2x=1+√3x=1−√3
^HT^
Ta thấy x=0 không là nghiệm của phương trình
chia cả 2 vế cho x^2 ta được:
PT <=> x^2-3x-6+3/x+1/(x^2)=0
<=> (x^2-2+1/(x^2))-3(x-1/x)-4=0
<=> (x-1/x)^2-3(x-1/x)-4=0
Đặt x-1/x=y
PT <=> y^2-3y-4=0
<=> y=-4 hoặc y=1
Tại y=-4 , ta có x+1/x+4=0
<=> x^2+4x+1=0
<=> x=-2+ √3 hoăc x=-2- √ 3
Tại y=1 ta có x^2-x-1=0
<=> x=(1- √ 5)/2 hoặc x=(1+ √5)/2
Đạo hàm y 0 −3x 2 + 6x + m − 1. Hàm số đã cho đồng biến trên khoảng (0; 3) khi và chỉ khi y 0 0, ∀x ∈ (0; 3). Hay −3x 2 + 6x + m − 1 0, ∀x ∈ (0; 3) ⇔ m 3x 2 − 6x + 1, ∀x ∈ (0; 3) (∗). Xét hàm số f(x) 3x 2 − 6x + 1 trên đoạn [0; 3] có f 0 (x) 6x − 6; f 0 (x) 0 ⇔ x 1. Khi đó f(0) 1, f(3) 10, f(1) −2, suy ra max [0;3] f(x) f(3) 10. Do đó (∗) ⇔ m max [0;3] f(x) ⇔ m 10. Vậy với m 10 thì hàm số đã cho đồng biến trên khoảng (0; 3).
Đọc tiếp
Đạo hàm y 0 = −3x 2 + 6x + m − 1. Hàm số đã cho đồng biến trên khoảng (0; 3) khi và chỉ khi y 0 > 0, ∀x ∈ (0; 3). Hay −3x 2 + 6x + m − 1 > 0, ∀x ∈ (0; 3) ⇔ m > 3x 2 − 6x + 1, ∀x ∈ (0; 3) (∗). Xét hàm số f(x) = 3x 2 − 6x + 1 trên đoạn [0; 3] có f 0 (x) = 6x − 6; f 0 (x) = 0 ⇔ x = 1. Khi đó f(0) = 1, f(3) = 10, f(1) = −2, suy ra max [0;3] f(x) = f(3) = 10. Do đó (∗) ⇔ m > max [0;3] f(x) ⇔ m > 10. Vậy với m > 10 thì hàm số đã cho đồng biến trên khoảng (0; 3).
cho biểu thức : A=( 3x+1/3x-1 - 3x-1/3x+1): 3x/ 6x-2.
a) Rút gọn A
b) Tìm x để A=1
c) Tìm x để A>0