P/s: Hình vẽ chỉ để giúp nhìn rõ vấn đề hơn nhưng độ chính xác không cao

a) Vì BI là tia phân giác của góc ABC

\(\Rightarrow\widehat{IBC}=\dfrac{\widehat{ABC}}{2}\left(1\right)\)

Vì CI là tia phân giác của góc ACB

\(\Rightarrow\widehat{ICB}=\dfrac{\widehat{ACB}}{2}\left(2\right)\)

Từ (1) và (2) suy ra

\(\widehat{IBC}+\widehat{ICB}=\dfrac{\widehat{ABC}}{2}+\dfrac{\widehat{ACB}}{2}=\dfrac{\widehat{ABC}+\widehat{ACB}}{2}\)

Vì \(\dfrac{\widehat{ABC}+\widehat{ACB}}{2}< \widehat{ABC}+\widehat{ACB}\)

\(\Rightarrow\widehat{IBC}+\widehat{ICB}< \widehat{ABC}+\widehat{ACB}\)

b) Vì \(\widehat{A}=60^0\)

\(\Rightarrow\widehat{ABC}+\widehat{ACB}=180^0-60^0=120^0\)

Hay \(\widehat{IBC}+\widehat{IBA}+\widehat{ICB}+\widehat{ICA}=120^0\)

\(\Rightarrow2\widehat{IBC}+2\widehat{ICB}=120^0\)

\(\Rightarrow2\left(\widehat{IBC}+\widehat{ICB}\right)=120^0\)

\(\Rightarrow\widehat{IBC}+\widehat{ICB}=60^0\)

Ta có: \(\widehat{IBC}+\widehat{ICB}+\widehat{BIC}=180^0\)

\(\Rightarrow60^0+\widehat{BIC}=180^0\)

\(\Rightarrow\widehat{BIC}=180^0-60^0=120^0\)

Bài 3: 

góc C=90-55=35 độ

Bài 1:

góc IBC=góc ABC/2=40 độ

góc ICB=40/2=20 độ

=>góc IBC+góc ICB=60 độ

=>góc BIC=120 độ

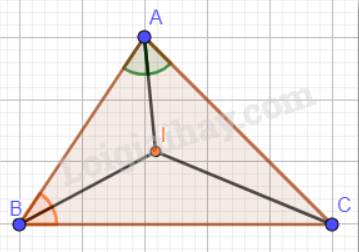
Ta có: I là giao điểm của hai đường phân giác góc A và góc B nên suy ra: CI là đường phân giác của góc C.

Vậy \(\widehat {ICA} = \widehat {ICB}\) ( tính chất tia phân giác của một góc).

Đáp án: A. \(\widehat {ICA} = \widehat {ICB}\).

a) I là giao điểm của ba đường phân giác tại ba góc A, B, C nên:

     \(\widehat {IAB} = \widehat {IAC};\widehat {IBA} = \widehat {IBC};\widehat {ICB} = \widehat {ICA}\).

Tổng ba góc trong một tam giác bằng 180° nên:

     \(\begin{array}{l}\widehat {BAC} + \widehat {ACB} + \widehat {CBA} = 180^\circ \\\widehat {IAB} + \widehat {IAC} + \widehat {IBA} + \widehat {IBC} + \widehat {ICB} + \widehat {ICA} = 180^\circ \\2\widehat {IAB} + 2\widehat {IBC} + 2\widehat {ICA} = 180^\circ \end{array}\)

Vậy \(\widehat {IAB} + \widehat {IBC} + \widehat {ICA} = 90^\circ \).

b) Tổng ba góc trong một tam giác bằng 180°. Xét tam giác BIC:

\(\begin{array}{l}\widehat {BIC} + \widehat {IBC} + \widehat {ICB} = 180^\circ \\\widehat {BIC} = 180^\circ  - (\widehat {IBC} + \widehat {ICB})\end{array}\).

Mà  \(\widehat {IAB} + \widehat {IBC} + \widehat {ICA} = 90^\circ \)→ \(\widehat {IBC} + \widehat {ICA} = 90^\circ  - \widehat {IAB}\).

Vậy: \(\begin{array}{l}\widehat {BIC} = 180^\circ  - (\widehat {IBC} + \widehat {ICB})\\\widehat {BIC} = 180^\circ  - (90^\circ  - \widehat {IAB})\\\widehat {BIC} = 90^\circ  + \widehat {IAB}\end{array}\)

Mà \(\widehat {IAB} = \dfrac{1}{2}\widehat {BAC}\)(IA là phân giác của góc BAC).

Vậy \(\widehat {BIC} = 90^\circ  + \widehat {IAB} = 90^\circ  + \dfrac{1}{2}\widehat {BAC}\). 

nhanh lên mình cần gấp lắm

giúp mình với huhuhuhuhuhuhuhuhuhuhuhuhuhuhuhuhuhu

Chịu lớp6

Chịu

vì BI là tia phân giác của ^ABC => ^ ABI = ^ IBC= ^ ABC / 2 = 80 / 2 =40

=>^IBC=40

vì CI là tia phân giác của ^ACB => ^ACI = ^ ICB = ACB / 2 = 40 / 2 = 20

=>^ICB = 20

Ta có : ^BIC+^IBC+^ICB= 180 ( tổng ba góc của 1 tam giác )

=> ^BIC +40+20 =180

=>^BIC = 120

mình ko vẽ đc hình , thông cảm . mà nếu đúng thì nhớ k !