B2 Phân tích thành hằng đẳng thức với a^2 +b^2 = hệ số còn lại

Những câu hỏi liên quan
Câu 1: Phân tích đa thức 8 - x3 thành nhân tử được?
Câu 2: Cho đẳng thức x2 - 5x + 4 = (x-1).B
Trong đó B là 1 hằng đẳng thức.
Khi đó hệ số tự do của đa thức B là?
Câu 1:8-x^3=2^3-x^3=(2-x)(4+2x+x^2)
Câu 2:Ta có:x^2-5x+4
=(x^2-2x5/2+25/4)-9/4
=(x-5/2)^2-(3/2)^2
=(x-5/2-3/2)(x-5/2+3/2)
=(x-4)(x-1)
->đa thức B là:(x-4)
->hệ số tự do của đa thức B là:-4
Đúng 0
Bình luận (0)
phân tích các đa thức sau thành nhân tử bằng phương pháp dùng hằng đẳng thức:
a) ( 4x^2 -3x -18 )^2 - ( 4x^2 +3x)^2
b) [ 4abcd +( a2+ b2) ( c2 +d2) ]2 -4[ cd (a2 + b2) +ab (c2 + d2)]2
Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức:
16 - ( a-b)2
\(=\left(4-a+b\right)\left(4+a-b\right)\)
Đúng 0
Bình luận (1)
Phân tích đa thức thành nhân tử bằng hằng đẳng thức
a) a2y2+b2x2- 2abxy
b) 100 - (3x-y)2
\(a,a^2y^2+b^2x^2-2abxy\\ =\left(ay\right)^2-2abxy+\left(bx\right)^2\\ =\left(ay-bx\right)^2=\left(bx-ay\right)^2\\ ---\\ b,100-\left(3x-y\right)^2\\ =10^2-\left(3x-y\right)^2\\ =\left(10-3x+y\right)\left(10+3x-y\right)\)
Đúng 3
Bình luận (0)
a) \(=\left(ay\right)^2-2abxy+\left(bx\right)^2\)
\(=\left(ay-bx\right)^2\)
b) \(100-\left(3x-y\right)^2\)
\(=10^2-\left(3x-y\right)^2\)
\(=\left(10-3x+y\right)\left(10+3x-y\right)\)
Đúng 2
Bình luận (0)
phân tích đa thức sau thành nhân tửvs phương pháp hằng đẳng thức
(2a-b)^2 - 4(a-b)^2
\(\left(2a-b\right)^2-4\left(a-b\right)^2\)
\(=\left(2a\right)^2-2.2a.b+b^2-4.a^2-2.a.b+b^2\)
\(=4a^2-4ab+b^2-4a^2-2ab+b^2\)
\(=-6ab+2b^2\)
Đúng 0
Bình luận (0)
\(\left(2a-b\right)^2-4\left(a-b\right)^2=4a^{^2}-4ab+b^2-4\left(a^2-2ab+b^2\right)=4a^2-4ab+b^2-4a^2+8ab-4b^2=4ab-3b^2=b\left(4a-3b\right)\)
Đúng 0
Bình luận (0)
Để tính giá trị biểu thức 20212 – 212 theo phương pháp dùng hằng đẳng thức thì áp dụng hằng đẳng thức nào sau đây?A. (A – B)2 A2 – 2AB + B2 B. (A + B)2 A2 + 2AB + B2C. A2 – B2 (A + B)(A – B) D. A3 – B3 (A – B)(A2 + AB + B2)
Đọc tiếp
Để tính giá trị biểu thức 20212 – 212 theo phương pháp dùng hằng đẳng thức thì áp dụng hằng đẳng thức nào sau đây?
A. (A – B)2 = A2 – 2AB + B2
B. (A + B)2 = A2 + 2AB + B2
C. A2 – B2 = (A + B)(A – B)
D. A3 – B3 = (A – B)(A2 + AB + B2)
Với a, b là hai số bất kì, trong các đẳng thức sau, đẳng thức nào không phải hằng đẳng
thức?
A. (a+b)2 =a2 +2ab+b2 B. a2 – 1 =3a C. a(2a+b) =2a2 + ab D. a(b+c) =ab+ac
phân tích câu sau thành nhân tử dùng hằng đẳng thức
a^2b - b^2 (x+y)^2
\(a^{2b}-b^2.\left(x+y\right)^2=\left(a^b\right)^2-\left(b\left(x+y\right)\right)^2=\left(a^b+bx+by\right)\left(a^b-bx-by\right)\)
Đúng 0
Bình luận (0)
Tính tích x.y, biết rằng x và y thỏa mãn các đẳng thức sau (a, b là các hằng số):
2
a
3
-
2
b
3
x
-
3
b
3
a
; với a
≠
b và
6
a
+
6
b...
Đọc tiếp
Tính tích x.y, biết rằng x và y thỏa mãn các đẳng thức sau (a, b là các hằng số): 2 a 3 - 2 b 3 x - 3 b = 3 a ; với a ≠ b và 6 a + 6 b y = a - b 2 với a ≠ - b
Vì a
≠
b nên
2
a
3
-
2
b
3
≠
0. Suy ra: 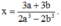
Vì a
≠
- b nên a + b
≠
0. Suy ra: 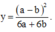
Vậy 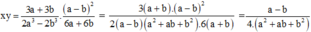
Đúng 0
Bình luận (0)
























