Trên đường thẳng \(\widehat{x'ox}\) trên nửa mặt phẳng bờ chứa \(\widehat{x'ox}\), người ta lấy 3 tia Oa, Ob, Oc sao cho \(\widehat{xoc}\)=2.\(\widehat{xob}\)=3.\(\widehat{xoa}\).
a) tìm giá trị lớn nhất của số đo \(\widehat{xoa}\)
b)Gọi Om là tia phân giác của \(\widehat{aOc}\). Trong 3 tia Oa, Ob, Oc tia nào nằm giữa 2 tia còn lại ?
c)cho \(\widehat{xoc}\)= 120 độ. Tính \(\widehat{bom}\). Tia OA là tia phân giác của góc nào ?
Cho \(\widehat{AOB}\) vuông và tia OC nằm trong góc đó. Vẽ tia OX sao cho OA là tia phân giác của \(\widehat{xOC}\), vẽ tia Oy sao cho OB là tia phân giác của \(\widehat{yOC}\). Chứng tỏ Ox, Oy là hai tia đối nhau.
\(\widehat{xOA}=\widehat{cOA}\) (gt) (1)
\(\widehat{yOB}=\widehat{COB}\) (gt) (2)
\(\widehat{COA}+\widehat{COB}=\widehat{AOB}=90^o\) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{xOA}+\widehat{yOB}=90^o\)
\(\Rightarrow\widehat{xOy}=\widehat{COA}+\widehat{COB}+\widehat{xOA}+\widehat{yOB}=90^o+90^o=180^o\)
=> Ox và Oy là hai tia đối nhau
Trên cùng nửa mặt phẳng bờ chứa tia Õ. Vẽ 2 tia OA và OB sao cho \(\widehat{xOA}\)= 680 ; \(\widehat{xOB}\) = 1360
a,Trong 3 tia Ox,OA,OB tia nào nằm giữa 2 tia còn lại?
b, Tính \(\widehat{AOB}\)
c, Tia OA có là tia phân giác của góc \(\widehat{xOB}\) không?
d, Vẽ tia Ot là tia phân giác của \(\widehat{AOB}\) . Tính \(\widehat{AOt}\) ;\(\widehat{BOt}\)
Vẽ hai góc kề bù \(\widehat {xOy},\widehat {yOx'}\), biết \(\widehat {xOy} = 120^\circ \). Gọi Oz là tia phân giác của \(\widehat {xOy}\), Oz’ là tia phân giác của \(\widehat {yOx'}\). Tính \(\widehat {zOy},\widehat {yOz'},\widehat {zOz'}\).
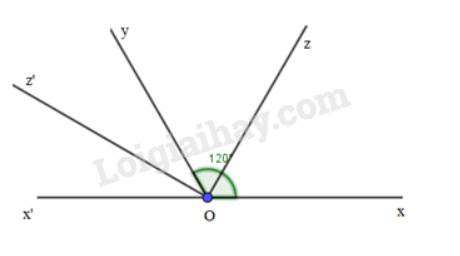
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.120^\circ = 60^\circ \)
Vì Oz’ là tia phân giác của \(\widehat {yOx'}\) nên \(\widehat {x'Oz'} = \widehat {yOz'} = \frac{1}{2}.\widehat {yOx'} = \frac{1}{2}.60^\circ = 30^\circ \)
Vì tia Oy nằm trong \(\widehat {zOz'}\) nên \(\widehat {zOz'}=\widehat {zOy} + \widehat {yOz'} = 60^\circ + 30^\circ = 90^\circ \)
Vậy \(\widehat {zOy} = 60^\circ ,\widehat {yOz'} = 30^\circ ,\widehat {zOz'} = 90^\circ \)
Chú ý:
2 tia phân giác của 2 góc kề bù thì vuông góc với nhau
Bài 2: (Vẽ hình) Cho \(\widehat{xOy}\). Trên tia \(Ox\) lấy điểm \(A\), trên tia \(Oy\) lấy điểm \(B\) sao cho \(OA=OB\). Gọi \(C\) là 1 điểm trên tia phân giác \(Oz\) của \(\widehat{xOy}\). Chứng minh rằng:
a, \(AC=BC\)
\(\widehat{xAC}=\widehat{yBC}\)
b, \(OC=OB\)
`a,`
Xét $\Delta OAC$ và $\Delta ABC$ ta có `:`
`OA=OB(gt)`
\(\widehat{AOC}=\widehat{BOC}\) `( Oz` là tia phân giác \(\widehat{B}\) `)`
Chung `Oz`
`=>` $\Delta OAC$ `=` $\Delta ABC$ `(c.g.c)`
`=>` `{(\hat{OAC}=\hat{OBC} \text{( 2 góc tương ứng )} ),(AC=BC \text{ (2 cạnh tương ứng)}):}`
Từ `\hat{OAC}=\hat{OBC}`
`=>` `\hat{xAC}=\hat{yBC}` `(` kề bù với `2` góc bằng nhau `)`
`b,` Xem lại đề bài `: OC=OB?`
Cho \(\widehat{xOy}\)= 70 độ.Gọi góc Ox',Oy' lần lượt là tia đối của tia Õ,Oy.Kẻ Oa là tia phân giác của \(\widehat{xOy}\).Ob là tia đối của tia Oa.Chứng tỏ Ob là tia phân giác của \(\widehat{x'Oy'}\)
do Oa là tia phân giác của góc xOy=> góc xOa= góc aOy = 70/2 = 35 độ
do Oy' là tia đối của tia Oy => góc xOy'+góc xOy = 180 độ => góc xOy' = 180-70 = 110
Do Ob tia đối của Oa => góc bOy' + góc y'Oa = 180 độ => góc bOy' + góc y'Ox+ góc xOa = 180 độ
=> góc bOy' + 110 độ + 35 độ =180 độ => góc bOy' = 35 độ
mà góc y'Ox' = góc xOy = 70 độ ( vì đối đỉnh)
=> Ob là tia phân giác
Do Oa là tia phân giác của góc xOy
=> góc xOa= góc aOy = góc xOa . \(\frac{1}{2}\) =70. \(\frac{1}{2}\) =35o
có góc xOy và góc x'Oy là hai góc kề bù
=> góc xOy + góc x'Oy=180 o
Thay số: 70o+ góc x'Oy=180o
góc x'Oy=180o-70o
góc x'Oy=1100
có góc x'Oy và x'Oy' là hai góc kề bù
=> góc x'Oy + x'Oy'=180o
Thay số: 110o+ góc x'Oy'=180o
góc x'Oy'=180o-110o
góc x'Oy'=70o
Có tia Ox nằm giữa 2 tia Oa và Oy'
=>góc aOx+ góc xOy'=góc aOy'
Thay số: 35o+110o=góc aOy'
góc aOy'=110o+35o
góc aOy'=145o
có góc bOy' và góc aOy' là 2 góc kề nhau
=> góc bOy'+ góc aOy'=180o
Thay số: góc bOy'+145o=180o
góc bOy'=180o-145o
góc bOy'=35o
có Ob nằm giữa 2 tia Ox' và Oy'
=> góc x'Ob+ góc bOy'=x'Oy'
Thay số: góc x'Ob +35o=70o
góc x'Ob=70o-35o
góc x'Ob=35o
góc x'Ob=góc bOy'=35o (1)
Tia Ob nằm giữa hai tia Ox' và Oy' (2)
Từ (1) và (2)
Vậy tia Ob là phân giác cảu góc x'Oy'
Cho \(\widehat{xoy}\) = 100o. Vẽ tia Oz là tia đối cua rtia Ox.Gọi Ot là tia phân giác của \(\widehat{yoz}\). Tính \(\widehat{yot}\), \(\widehat{xot}\)
Vẽ góc bẹt \(\widehat {xOy}\). Vẽ tia phân giác Oz của góc đó. Vẽ tia phân giác Ot của \(\widehat {xOz}\). Vẽ tia phân giác Ov của \(\widehat {zOy}\) . Tính \(\widehat {tOv}\).
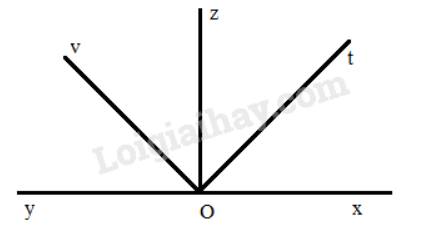
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy}\) = \(\frac{1}{2}.180^\circ = 90^\circ \)
Vì Ot là tia phân giác của \(\widehat {xOz}\) nên \(\widehat {xOt} = \widehat {tOz} = \frac{1}{2}\widehat {xOz} = \frac{1}{2}.90^\circ = 45^\circ \)
Vì Ov là tia phân giác của \(\widehat {zOy}\) nên \(\widehat {yOv} = \widehat {vOz} = \frac{1}{2}\widehat {zOy} = \frac{1}{2}.90^\circ = 45^\circ \)
Mà tia Oz nằm trong \(\widehat {tOv}\) nên \(\widehat {tOv}= \widehat {tOz} + \widehat {zOv} = 45^\circ + 45^\circ = 90^\circ \)
Vậy \(\widehat {tOv} = 90^\circ \)
Cho \(\widehat{xOy,}\) là 2 góc kề bù. Oa là tia phân giác của \(\widehat{xOy}\), Ob là tia phân giác của \(\widehat{yOz}\)
Chứng minh rằng: Oa vuông góc với Ob
\(\widehat{aOy}=\dfrac{\widehat{xOy}}{2}\)
\(\widehat{bOy}=\dfrac{\widehat{zOy}}{2}\)
Do đó: \(\widehat{aOy}+\widehat{bOy}=\dfrac{1}{2}\left(\widehat{xOy}+\widehat{yOz}\right)=\dfrac{1}{2}\cdot180^0\)
hay \(\widehat{aOb}=90^0\)(đpcm)
