cho đa thức P(x) = ax3 + bx2 + cx + d ( a # 0 ) , bt :
P(1) = 100
P(-1) = 50
P(0) = 1
P(2)= 120
Tính P ( 3 )
Cho đa thức: f(x)=x4+ax3+bx2+cx+df(x)=x4+ax3+bx2+cx+d ( với a, b, c, d là các số thực). Biết f(1)=10; f(2)=20; f(3)=30. Tính giá trị của biểu thức: A=f(9)+f(-5
)
Đặt \(g\left(x\right)=f\left(x\right)-10\) (bậc 4)
\(\Leftrightarrow\left\{{}\begin{matrix}g\left(1\right)=0\\g\left(2\right)=0\\g\left(3\right)=0\end{matrix}\right.\Leftrightarrow g\left(x\right)=\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-m\right)\) (m là hằng số)
\(\Leftrightarrow f\left(x\right)=\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-m\right)-10\\ \Leftrightarrow f\left(9\right)=8\cdot7\cdot6\left(9-m\right)-10=336\left(9-m\right)-10\\ f\left(-5\right)=\left(-6\right)\left(-7\right)\left(-8\right)\left(-5-m\right)-10=336\left(m+5\right)-10\)
Vậy \(A=336\left(9-m\right)+336\left(m+5\right)-20=4684\)
Chúc bạn hok tốt <3
tìm n ϵZ sao cho (2n-3):(n+1)
b)cho đa thức: P(x)=ax3-bx2+cx+d. với P (0) và P(1) là số lẻ
Yêu cầu đề bài có vẻ không rõ ràng lắm, bạn viết lại được không?
a, n \(\in\) Z sao cho (2n - 3) \(⋮\) (n+1)
2n + 2 - 5 ⋮ n + 1
2(n+1) - 5 ⋮ n + 1
5 ⋮ n + 1
n + 1 \(\in\) { -5; -1; 1; 5}
n \(\in\) { -6; -2; 0; 4}
Ý b đề ko rõ ràng em nhé
cho đa thức P(x)=ax3+bx2+cx+d .Với P(0) và P(1) là số lẻ . Chứng minh rằng P(x) không thể có nghiệm là số nguyên
Lời giải:
$P(0)=d$ lẻ
$P(1)=a+b+c+d$ lẻ, mà $d$ lẻ nên $a+b+c$ chẵn. Do đó 3 số này có thể nhận giá trị lẻ, lẻ, chẵn hoặc chẵn, chẵn, chẵn.
Giả sử $P(x)$ có nghiệm nguyên $m$. Khi đó:
$P(m)=am^3+bm^2+cm+d$
Nếu $m$ chẵn thì $am^3+bm^2+cm+d$ lẻ cho $d$ lẻ nên $P(m)\neq 0$
Nếu $m$ lẻ: Do $a,b,c$ nhận giá trị lẻ, chẵn, chẵn hoặc chẵn, chẵn, chẵn nên $am^3+bm^2+cm$ đều chẵn. Kéo theo $P(m)=am^3+bm^2+cm+d$ lẻ
$\Rightarrow P(m)\neq 0$
Tóm lại $P(m)\neq 0$
$\Rightarrow x=m$ không là nghiệm của $P(x)$. Do đó điều giả sử là sai.
Ta có đpcm.
cho đa thức bậc 3 f(x) = ax3 +bx2 + cx +d với a là số nguyên dương. Biết rằng f(5) - f(4) = 2020. CMR: f(7) - f(2) là hợp số
Hỏi có bao nhiêu đa thức bậc ba P(x) =ax3+bx2+cx+d mà các hệ số a, b, c, d thuộc tập {-3,-2,0,2,3}. Biết rằng:
a/Các hệ số tùy ý.
A. 3125
B. 625
C. 500
D. 360
Khi các hệ số tùy ý; ta cần thực hiện các bước sau:
Chọn hệ số a: có 4 cách chọn hệ số a vì a≠0.
Chọn hệ số b: có 5 cách chọn hệ số b.
Chọn hệ số c: có 5 cách chọn hệ số c
Chọn hệ số d: có 5 cách chọn hệ số d.
Theo quy tắc nhân có: 4.5.5.5=500 đa thức.
Chọn C.
Cho đa thức P(x) = ax3 + bx2 + cx + d với a, b, c, d là các hệ số nguyên. Chứng minh rằng nếu P(x) chia hết cho 5 với mọi giá trị nguyên của x thì các hệ số a, b, c, d đều chia hết cho 5
Hỏi có bao nhiêu đa thức bậc ba P(x) =ax3+bx2+cx+d mà các hệ số a, b, c, d thuộc tập {-3,-2,0,2,3}. Biết rằng:
b/Các hệ số đều khác nhau.
A: 525
B: 96
C: 192
D:384
Khi các hệ số khác nhau:
- Có 4 cách chọn hệ số a (a≠0).
- Khi đã chọn a, có 4 cách chọn b.
- Khi đã chọn a và b, có 3 cách chọn c.
- Khi đã chọn a, b và c có 2 cách chọn d.
Theo quy tắc nhân ta có. 4.4.3.2=96 đa thức.
Chọn B.
cho đa thức f(x) = ax3 + bx2 + cx + 2021 với a nguyên dương .biết rằng f(5) - f(4)= 2020Chứng minh rằng f(7) - f(2) là hợp số
Ta có: \(\left\{{}\begin{matrix}f\left(5\right)=125a+25b+5c+2021\\f\left(4\right)=64a+16b+4c+2021\end{matrix}\right.\)
\(f\left(5\right)-f\left(4\right)=2020\) \(\Rightarrow61a+9b+c=2020\)
Ta có: \(\left\{{}\begin{matrix}f\left(7\right)=343a+49b+7b+2021\\f\left(2\right)=8a+4b+2c+2021\end{matrix}\right.\)
\(\Rightarrow f\left(7\right)-f\left(2\right)=335a+45b+5b=5\left(61a+9b+c\right)=5.2020\)
\(\Rightarrow f\left(7\right)-f\left(2\right)\) chia hết cho 5 nên nó là hợp số.
1.Tìm nghiệm đa thức
1)6x3 - 2x2
2)|3x + 7| + |2x2 - 2|
2.Chứng minh đa thức ko có nghiệm
1)x2 + 2x + 4
2)3x2 - x + 5
3.Tìm các hệ số a, b, c, d của đa thức f(x) = ax3 + bx2+ cx + d
Biết f(0)=5; f(1)=4; f(2)=31; f(3)=88
Bài 1:
1.
$6x^3-2x^2=0$
$2x^2(3x-1)=0$
$\Rightarrow 2x^2=0$ hoặc $3x-1=0$
$\Rightarrow x=0$ hoặc $x=\frac{1}{3}$
Đây chính là 2 nghiệm của đa thức
2.
$|3x+7|\geq 0$
$|2x^2-2|\geq 0$
Để tổng 2 số bằng $0$ thì: $|3x+7|=|2x^2-2|=0$
$\Rightarrow x=\frac{-7}{3}$ và $x=\pm 1$ (vô lý)
Vậy đa thức vô nghiệm.
Bài 2:
1. $x^2+2x+4=(x^2+2x+1)+3=(x+1)^2+3$
Do $(x+1)^2\geq 0$ với mọi $x$ nên $x^2+2x+4=(x+1)^2+3\geq 3>0$ với mọi $x$
$\Rightarrow x^2+2x+4\neq 0$ với mọi $x$
Do đó đa thức vô nghiệm
2.
$3x^2-x+5=2x^2+(x^2-x+\frac{1}{4})+\frac{19}{4}$
$=2x^2+(x-\frac{1}{2})^2+\frac{19}{4}\geq 0+0+\frac{19}{4}>0$ với mọi $x$
Vậy đa thức khác 0 với mọi $x$
Do đó đa thức không có nghiệm.
Bài 3:
$f(0)=a.0^3+b.0^2+c.0+d=d=5$
$f(1)=a+b+c+d=4$
$a+b+c=4-d=-1(*)$
$f(2)=8a+4b+2c+d=31$
$8a+4b+2c=31-d=26$
$4a+2b+c=13(**)$
$f(3)=27a+9b+3c+d=88$
$27a+9b+3c=88-d=83(***)$
Từ $(*); (**); (***)$ suy ra $a=\frac{1}{3}; b=13; c=\frac{-43}{3}$
Vậy.......
Cho hàm số y = a x 3 + b x 2 + c x + d có đồ thị như hình bên. Hỏi phương trình a x 3 + b x 2 + c x + d = 0 có bao nhiêu nghiệm?
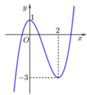
A. Phương trình không có nghiệm
B. Phương trình có đúng một nghiệm
C. Phương trình có đúng hai nghiệm
D. Phương trình có đúng ba nghiệm