Có hình vẽ : 

Dễ thấy S_ABCD = \(\frac{1}{2}\left(AH+CK\right).BD\)

mà lại có \(AH=AO.sin\alpha\) ; \(CK=OC.sin\alpha\)

=> S_ABCD = \(\frac{1}{2}\sin\alpha.AC.BD\)

Khi 2 đường chéo vuông góc với nhau thì 

\(H\equiv O\equiv K\Rightarrow AH=AO=CK\)

hay \(sin\alpha=1\)

Khi đó \(S_{ABCD}=\frac{1}{2}mn\)(đpcm) 

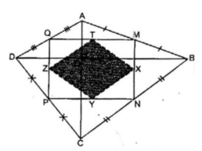
Kẻ đường chéo MP và NQ

Trong  △ MNP ta có:

X là trung điểm của MN

Y là trung điểm của NP

nên XY là đường trung bình của  △ MNP

⇒ XY // MP và XY = 1/2 MP (tính chất đường trung bình của tam giác) (3)

Trong  △ QMP ta có:

T là trung điểm của QM

Z là trung điểm của QP

nên TZ là đường trung bình của  △ QMP

⇒ TZ // MP và TZ = 1/2 MP (tính chất đường trung bình của tam giác) (4)

Từ (3) và (4) suy ra: XY // TZ và XY = TZ nên tứ giác XYZT là hình bình hành.

Trong △ MNQ ta có XT là đường trung bình

⇒ XT = 1/2 QN (tính chất đường trung bình của tam giác)

Tứ giác MNPQ là hình chữ nhật ⇒ MP = NQ

Suy ra: XT = XY. Vậy tứ giác XYZT là hình thoi

S X Y Z T  = 1/2 XZ. TY

mà XZ = MQ = 1/2 BD = 1/2. 8 = 4 (cm);

TY = MN = 1/2 AC = 1/2 .6 =3 (cm)

Vậy : S X Y Z T  = 1/2. 3. 4 = 6( c m 2 )

Mik kb nha