A

Cho hai tam giác ABC và DEF .có BC = EF ; AB = DE ; AC = DF . Ta có:

  A.  ∆ ABC =  ∆ DEF                 B.  ∆ ABC =  ∆ EDF 

 C.  ∆ CAB =  ∆ DFE                 D.  ∆ BAC =  ∆ DFE 

A nha bn

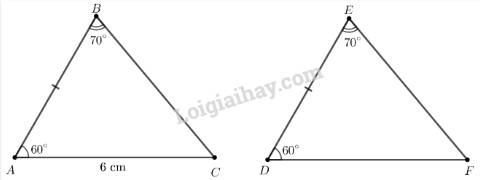
Xét hai tam giác ABC và DEF có:

\(\begin{array}{l}\widehat {ABC} = \widehat {DEF} (= {70^\circ })\\AB = DE\\\widehat {BAC} = \widehat {EDF} (= {60^\circ })\end{array}\)

\( \Rightarrow \Delta ABC{\rm{  = }}\Delta DEF\)(g.c.g)

\( \Rightarrow DF = AC\)( 2 cạnh tương ứng)

Mà AC = 6 cm

\( \Rightarrow DF = 6cm\)

\(\Delta DEF\) cho ta \(\widehat{D}+\widehat{E}+\widehat{F}=180^0\)

                   \(\Rightarrow\widehat{D}=180^0-\left(\widehat{E}+\widehat{F}\right)\)

                   \(\Rightarrow\widehat{D}=180^0-\left(70^0+60^0\right)=180^0-130^0=50^0\)

\(Xét\) \(\Delta ABCvà\Delta DEFcó\)

\(\widehat{A}=\widehat{D}\left(=50^0\right)\)

AB=DE

AC=DF

\(\Rightarrow\Delta ABC=\Delta DEF\left(c-g-c\right)\)

Vậy \(\Delta ABC=\Delta DEF\)

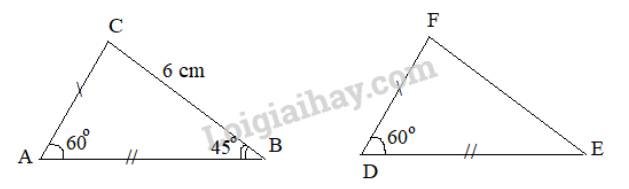
Xét hai tam giác ABC và DEF có:

\(\begin{array}{l}AB = DE\\AC = DF\\\widehat {BAC} = \widehat {EDF} (= {60^\circ })\end{array}\)

\(\Rightarrow \Delta ABC = \Delta DEF\)(c.g.c)

Do đó:

\(BC=EF = 6cm\) ( 2 cạnh tương ứng)

\( \widehat {ABC} =\widehat {DEF}= {45^o}\) (2 góc tương ứng)

\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^o}\\ \Rightarrow {60^o} + {45^o} + \widehat {ACB} = {180^o}\\ \Rightarrow \widehat {ACB} = {75^o}\end{array}\)

\( \Rightarrow \widehat {EFD} = \widehat {ACB} = {75^o}\)

Đáp án C

Để tam giác ABC và tam giác DEF bằng nhau theo trường hợp cạnh – góc – cạnh cần thêm điều kiện về cạnh kề đó là:  A ^  =  D ^

-Đề sai.