\(4=x+y+z\ge3\sqrt[3]{xyz}\Leftrightarrow\sqrt[3]{xyz}\le\dfrac{4}{3}\Leftrightarrow xyz\le\dfrac{64}{27}\)(BĐT cauchy)

Dấu \("="\Leftrightarrow x=y=z=\dfrac{4}{3}\)

Lời giải:

Áp dụng BĐT AM-GM:
$xy\le \frac{(x+y)^2}{4}=\frac{(4-z)^2}{4}$

$\Rightarrow H\leq \frac{z(4-z)^2}{4}$

Tiếp tục áp dụng BĐT AM-GM:
$z(4-z)\leq \frac{(z+4-z)^2}{4}=4$

$4-z\leq 2$ do $z\geq 2$

$\Rightarrow \frac{z(4-z)^2}{4}\leq \frac{4.2}{4}=2$

Hay $H\leq 2$ 

Vậy $H_{\max}=2$ khi $(x,y,z)=(1,1,2)$

\(A=3yz+\left(4-y-z\right)\left(y+2z\right)\)

\(A=-y^2+4y-2z^2+8z\)

\(A=-\left(y-2\right)^2-2\left(z-2\right)^2+12\le12\)

\(A_{max}=12\) khi \(\left(x;y;z\right)=\left(0;2;2\right)\)

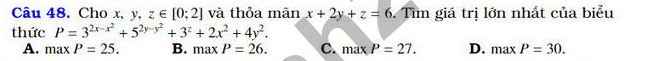
Do \(x;y\in\left[0;2\right]\Rightarrow\left\{{}\begin{matrix}x\left(2-x\right)\ge0\\y\left(2-y\right)\ge0\end{matrix}\right.\) \(\Rightarrow2x^2+4y^2\le4x+8y\)

\(P\le3^0+5^0+3^z+4\left(x+2y\right)=2+3^z+4\left(6-z\right)=3^z-4z+26\)

Xét hàm \(f\left(z\right)=3^z-4z+26\) trên \(\left[0;2\right]\)

\(f'\left(z\right)=3^z.ln3-4=0\Rightarrow z=log_3\left(\dfrac{4}{ln3}\right)=a\)

\(f\left(0\right)=27\) ; \(f\left(2\right)=27\); \(f\left(a\right)\approx-1,1\)

\(\Rightarrow f\left(z\right)\le27\Rightarrow maxP=27\)

(Dấu "=" xảy ra khi \(\left(x;y;z\right)=\left(0;2;2\right)\))

Ồ mà khoan, bài trước bị nhầm lẫn ở chỗ \(3^{2x-x^2}+5^{2y-y^2}\ge3^0+5^0\) mới đúng, ko để ý bị ngược dấu đoạn này

Vậy giải cách khác:

\(0\le x;y;z\le2\Rightarrow x\left(2-x\right)\ge0\Rightarrow2x-x^2\ge0\)

Lại có: \(2x-x^2=1-\left(x-1\right)^2\le1\)

\(\Rightarrow0\le2x-x^2\le1\)

Tương tự ta có: \(0\le2y-y^2\le1\)

Xét hàm: \(f\left(t\right)=3^t-2t\) trên \(\left[0;1\right]\)

\(f'\left(t\right)=3^t.ln3-2=0\Rightarrow t=log_3\left(\dfrac{2}{ln3}\right)=a\)

\(f\left(0\right)=1;\) \(f\left(1\right)=1\) ; \(f\left(a\right)\approx0,73\)

\(\Rightarrow f\left(t\right)\le1\Rightarrow3^t-2t\le1\Rightarrow3^t\le2t+1\)

\(\Rightarrow3^{2x-x^2}\le2\left(2x-x^2\right)+1\)

Hoàn toàn tương tự, ta chứng minh được: 

\(5^t\le4t+1\) với \(t\in\left[0;1\right]\Rightarrow5^{2y-y^2}\le4\left(2y-y^2\right)+1\)

\(3^t\le4t+1\) với \(t\in\left[0;2\right]\Rightarrow3^z\le4z+1\)

\(\Rightarrow P\le2\left(2x-x^2\right)+4\left(2y-y^2\right)+4z+3+2x^2+4y^2=4\left(x+2y+z\right)+3=27\)

Lần này thì ko sai được rồi

Tham khảo:

Cho 3 số thức x,y,z thỏa mãn \(x\ge1;y\ge4;z\ge9\) tìm giá trị lớn nhất của biết thức Q=\(\dfrac{yz\sqrt{x-1}+zx\sqrt... - Hoc24