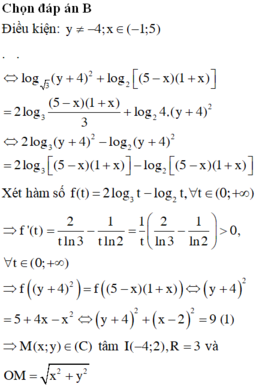Có bao nhiêu tập hợp S thỏa mãn : {7,8} là con của S và S là con của {3,7,8,9}

Những câu hỏi liên quan
Trong không gian Oxyz, cho điểm
M
2
;
-
3
;
4
. Gọi
P
là mặt phẳng đi qua M và cắt các trục
x
O
x
,
y
O
y
,
z
O
z
lần lượt tại các điểm D, E, F sao cho
O
D...
Đọc tiếp
Trong không gian Oxyz, cho điểm M 2 ; - 3 ; 4 . Gọi P là mặt phẳng đi qua M và cắt các trục x ' O x , y ' O y , z ' O z lần lượt tại các điểm D, E, F sao cho O D = 2 O E = m 2 - 2 m + 2 O F ≠ 0 , trong đó m là tham số thực. Gọi S là tập hợp các giá trị của m để chỉ có đúng ba mặt phẳng thỏa mãn yêu cầu trên.
Tập hợp S có bao nhiêu tập hợp con khác rỗng?
A. 7
B. 3
C. 15
D. 4
Chọn đáp án A.




Suy ra số tập hợp con khác rỗng của S là 2 3 - 1 = 7

Đúng 0
Bình luận (0)
có bao nhiêu tập S thỏa mãn: 7,8 thuộc S thuộc 1,7,9,8
CÓ BAO NHIÊU TẬP HỢP X THỎA MÃN {1;2} LÀ TẬP HỢP CON CỦA X MÀ X CŨNG LÀ TẬP HỢP CON CỦA {1;2;3;4;5}
có bao nhiêu tập hợp x thỏa mãn đk {c;d;e} là con của x và x là con của {a;b;c;d;e;f}
có bao nhiêu tập hợp x thỏa mãn: {1; 2} là con của x và x là con của {1; 2; 3; 4; 5} (nhớ ghi cách giải)
Cho hai số thực x, y thỏa mãn:
log
3
(
y
2
+
8
y
+
16
)
+
l
o
g
2
[(
5
−
x
)
(
1
+
x
)
]2log
3
5
+
4
x...
Đọc tiếp
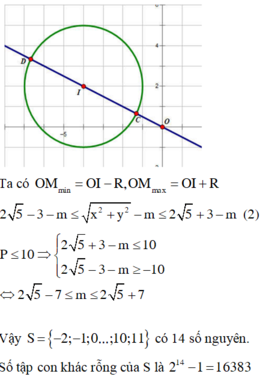
Cho hai số thực x, y thỏa mãn: log 3 ( y 2 + 8 y + 16 ) + l o g 2 [( 5 − x ) ( 1 + x ) ]=2log 3 5 + 4 x − x 2 3 + log 2 ( 2 y + 8 ) 2 . Gọi S là tập các giá trị nguyên của tham số m để giá trị lớn nhất của biểu thức P = x 2 + y 2 − m không vượt quá 10. Hỏi S có bao nhiêu tập con không phải là tập rỗng?
A. 2047
B. 16383
C. 16384
D. 32
Cho tập hợp A thỏa mãn
{ 5;6 } là con của M. M là con của { 5;6;7;8}
có bao nhiêu tập hợp M như thế
Tìm tất cả các tập hợp con S của \(ℤ+\) thỏa mãn: S là tập hữu hạn, khác rỗng, và với mọi a,b \(\in\)S thì \(\frac{a+b}{gcd\left(a,b\right)}\in S\).
(gcd là ước chung lớn nhất)
Cho tập hợp S có 12 phần tử. Hỏi có bao nhiêu cách chia tập hợp S thành hai tập con (không kể thứ tự) mà hợp của chúng bằng S ?
A
.
3
12
+
1
2
B
.
3
12
-
...
Đọc tiếp
Cho tập hợp S có 12 phần tử. Hỏi có bao nhiêu cách chia tập hợp S thành hai tập con (không kể thứ tự) mà hợp của chúng bằng S ?
A . 3 12 + 1 2
B . 3 12 - 1 2
C . 3 12 + 1
D . 3 12 - 1
Chọn A
Cách 1.
Giả sử ![]() Đặt
Đặt ![]() Khi đó
C
1
,
C
2
, C là ba tập con không giao nhau của S và S =
C
1
∪
C
2
∪
C
Khi đó
C
1
,
C
2
, C là ba tập con không giao nhau của S và S =
C
1
∪
C
2
∪
C
Khi đó mỗi phần tử x ∈ S có 3 khả năng: Hoặc thuộc tập C 1 hoặc thuộc tập C 2 hoặc thuộc tập C.
Do đó 12 phần tử sẽ có 3 12 cách chọn.
Trong các cách chọn nói trên có 1 trường hợp C 1 = C 2 = ∅ , C = S
Các trường hợp còn lại thì lặp lại 2 lần (đổi vai trò C 1 và C 2 cho nhau).
Do đó số cách chia là 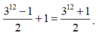
Cách 2.
Đặt S = S 1 ∪ S 2
Nếu
S
1
có k phần tử ![]()
![]()
![]()
![]()
Vậy số cách chọn 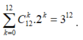
Nhưng trường hợp ![]() giống nhau và không hoán vị nên có
giống nhau và không hoán vị nên có  cách
cách
Đúng 0
Bình luận (0)