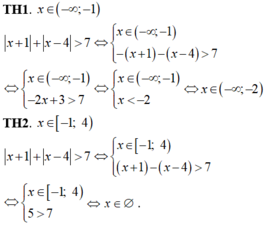Nghiệm nguyên nhỏ nhất của bất phương trình : \(\sqrt{x+1}< x+3\)

Những câu hỏi liên quan
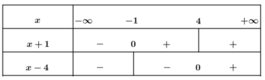
Giải bất phương trình
x
+
1
+
x
-
4
7
Giá trị nghiệm nguyên dương nhỏ nhất của x thoả mãn bất phương trình là A. x 9 B. x 8 C. x 6 D. x 7
Đọc tiếp
Giải bất phương trình x + 1 + x - 4 > 7
Giá trị nghiệm nguyên dương nhỏ nhất của x thoả mãn bất phương trình là
A. x = 9
B. x = 8
C. x = 6
D. x = 7
1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+30 và ( a+1)x-a+202/ Bất phương trình: 5x/5 - 13/21 + x/15 9/25- 2x/35 có nghiệm là....3/ Bất phương trình: 5x-1 2x/5 + 3 có nghiệm là...4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) (4x/3x-x^2) có nghiệm nguyên lớn nhất là...5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 2x -166/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 12 - 2x/37/ Bất phương trình: 2(x-1) - x 3(x-1) - 2x-5 có t...
Đọc tiếp
1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+3>0 và ( a+1)x-a+2>0
2/ Bất phương trình: 5x/5 - 13/21 + x/15 < 9/25- 2x/35 có nghiệm là....
3/ Bất phương trình: 5x-1 < 2x/5 + 3 có nghiệm là...
4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) < (4x/3x-x^2) có nghiệm nguyên lớn nhất là...
5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 < 2x -16
6/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 > 12 - 2x/3
7/ Bất phương trình: 2(x-1) - x > 3(x-1) - 2x-5 có tập nghiệm là...
8/ Bất phương trình: (3x+5/2) -1< (x+2/3)+x có tập nghiệm là...
9/ Bất phương trình: /x+2/ - /x-1/ < x - 3/2 có tập nghiệm là
10/ Bất phương trình: /x+1/ + /x-4/ > 7 có nghiệm nguyên dương nhỏ nhất là....
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
Mình không biết sin lỗi vạn
Xem thêm câu trả lời
nghiệm nguyên nhỏ nhất của bất phương trình \(\sqrt{x}\)>2 là
\(\sqrt{x}>2\) (ĐKXĐ: \(x\ge0\))
\(\Leftrightarrow x>4\). Vì x là số nguyên nhỏ nhất nên x = 5 thoả mãn bất phương trình.
Đúng 0
Bình luận (0)
Nghiệm nguyên nhỏ nhất của bất phương trình \(\sqrt{x}>2\) là x= ?
\(\sqrt{x}\)>2 <=> x>22 <=>x>4
Vậy nghiêm nhỏ nhất là 5
Đúng 0
Bình luận (0)
a) Tìm tất cả nghiệm nguyên dương của bất phương trình : \(11x-7< 8x+7\)
b) Tìm tất cả nghiệm nguyên âm của bất phương trình \(\frac{x^2+2x+8}{2}-\frac{x^2-x+1}{6}>\frac{x^2-x+1}{3}-\frac{x+1}{4}\)
c)Tìm nghiệm nguyên nhỏ nhất của bất phương trình : \(2\left(3-x\right)-1,5\left(x-4\right)< 3-x\)
a)11x-7<8x+7
<-->11x-8x<7+7
<-->3x<14
<--->x<14/3 mà x nguyên dương
---->x \(\in\){0;1;2;3;4}
b)x^2+2x+8/2-x^2-x+1>x^2-x+1/3-x+1/4
<-->6x^2+12x+48-2x^2+2x-2>4x^2-4x+4-3x-3(bo mau)
<--->6x^2+12x-2x^2+2x-4x^2+4x+3x>4-3+2-48
<--->21x>-45
--->x>-45/21=-15/7 mà x nguyên âm
----->x \(\in\){-1;-2}
c)2(3-x)-1,5(x-4)<3-x
<--->6-2x-1,5x+6<3-x
<--->6+6-3<2x+1,5x-x
<--->9<2,5x
<--->3,6<x mà x la so nguyen nhỏ nhất
--->x=4
Xem thêm câu trả lời
Tìm nghiệm nguyên nhỏ nhất của bất phương trình
log
3
(
1
-
x
2
)
≤
log
1
3
(
1
-
x
)
A. x0. B. x1 C. x -1 D. x 3
Đọc tiếp
Tìm nghiệm nguyên nhỏ nhất của bất phương trình
log 3 ( 1 - x 2 ) ≤ log 1 3 ( 1 - x )
A. x=0.
B. x=1
C. x= -1
D. x= 3
Chọn A
Điều kiện: -1< x< 1.
Ta có:
![]()
Bất phương trình đã cho tương đương:
log3( 1-x2) ≤ - log3(1-x) hay log3( 1-x2) + log3( 1-x)≤ 0.
=> log3[ ( 1-x2).( 1-x)]
=> (1-x2)( 1-x)≤ 1 ó 1-x-x2+ x3 ≤ 1
ó x3-x2- x≤ 0
![]()
ó x
Kết hợp với điều kiện; suy ra x=0 là nghiệm nguyên nhỏ nhất của bất phương trình..
Chọn A.
Đúng 0
Bình luận (0)
Nghiệm nguyên nhỏ nhất của bất phương trình \(\sqrt{x^2-16x+6}
pt<=>\(\sqrt{x^2-16x+64-58}\)=\(\sqrt{\left(x-8\right)^2+58}\)
=> gtnn= \(\sqrt{58}\)
khi x=8
Đúng 0
Bình luận (0)
Nghiệm nguyên nhỏ nhất của bất phương trình là
...
\(\sqrt{4x-1}\ge4\)
<=> \(\begin{cases}4x-1\ge0\\4x-1\ge16\end{cases}\)
<=>x>=1/4=> ngiệm nguyên nhỏ nhất là L: 1
Đúng 0
Bình luận (0)
Cho bất phương trình:
x
-
1
x
+
2
1
Nghiệm nguyên lớn nhất của bất phương trình là : A. -1 B. 2 C. -2 D. 1
Đọc tiếp
Cho bất phương trình: x - 1 x + 2 > 1
Nghiệm nguyên lớn nhất của bất phương trình là :
A. -1
B. 2
C. -2
D. 1
Chọn A
Điều kiện : x ≠ -2
TH1 : Nếu x< -2 ( vô lí)
TH2: Nếu -2, x< 1; bpt trở thành: 1-x> x+2
Hay x< -1/2
Kết hợp với điều kiện,ta có: -2< x< -1/2
TH3: Nếu x ≥ 1, bất phương trình trở thành: x-1> x+2 (vô lí)
Vậy bpt có tập nghiệm S= (-2; -1/2)
Nghiệm nguyên lớn nhất của bpt là -1
Đúng 0
Bình luận (0)
cho \(\sqrt{x+3}-\sqrt{7-x}>\sqrt{2x-8}\) số nghiệm nguyên của bất phương trình là:
giải giúp em với ạ
\(\sqrt{x+3}-\sqrt{7-x}>\sqrt{2x-8}\)
⇔ \(\sqrt{x+3}>\sqrt{7-x}+\sqrt{2x-8}\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\x+3>7-x+2x-8+2\sqrt{\left(7-x\right)\left(2x-8\right)}\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\x+3>x-1+2\sqrt{\left(7-x\right)\left(2x+8\right)}\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\4>2\sqrt{\left(7-x\right)\left(2x+8\right)}\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\\sqrt{\left(7-x\right)\left(2x-8\right)}< 2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\-2x^2+22x-56< 2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\\left[{}\begin{matrix}x>\dfrac{11+\sqrt{5}}{2}\\x< \dfrac{11-\sqrt{5}}{2}\end{matrix}\right.\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}4\le x< \dfrac{11-\sqrt{5}}{2}\\\dfrac{11+\sqrt{5}}{2}< x\le8\end{matrix}\right.\)
Các giá trị nguyên của x thỏa mãn là S = {4 ; 7 ; 8}
Đúng 1
Bình luận (0)
Ấy chết sai điều kiện XĐ rồi, bạn sửa lại điều kiện thôi nhé
Đúng 1
Bình luận (0)