Tìm m để hàm số y=mx3-x2+3x+m-2 đồng biến trên khoảng (-3;0)
A.[3;dương vô cùng)
B.(âm vô cùng;3)
C.(3/2;3)
D. (Âm vô cùng;3/2)
Những câu hỏi liên quan
Tìm m để hàm số y = 1 3 x 3 - x 2 - m x + 1 luôn đồng biến trên từng khoảng xác định của nó
A. m < - 1
B. m > -1
C. m ≤ -1
D. m > -1
Tìm tất cả các giá trị của tham số m để hàm số
y
(
m
2
-
1
)
x
4
-
2
m
x
2
đồng biến trên khoảng
(
1
;
+
∞
)
A.
m
≤
-
1
B. m -1 hoặc
m
1...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số y = ( m 2 - 1 ) x 4 - 2 m x 2 đồng biến trên khoảng ( 1 ; + ∞ )
A. m ≤ - 1
B. m = -1 hoặc m > 1 + 5 2
C. m ≤ - 1 hoặc m ≥ 1 + 5 2
D. m ≤ - 1 hoặc m > 1
Để hàm số
,
y
-
x
3
3
+
a
-
1
x
2
+
a
+
3
x...
Đọc tiếp
Để hàm số , y = - x 3 3 + a - 1 x 2 + a + 3 x - 4 đồng biến trên khoảng 0 ; 3 thì giá trị cần tìm của tham số a là:
A. a < - 3
B. a > - 3
C. - 3 < a < 12 7
D. a ≥ 12 7
Tìm m để hàm số y = x 3 - 3 m x 2 + 12 x - 2 nghịch biến trên khoảng (1; 4)
A. m ≥ 5/2
B. m ≤ 5/2
C. m ≤ 2
D. Đáp án khác
Cho hàm số bậc nhất y =- kx +k:^2+3 tìm k để đồ thị hàm số đồng biến trên R
Xem chi tiết
bn có thể viết rõ hơn được ko?
-kx + k^2 + 3 hay là gì?
Đúng 0
Bình luận (0)
Đề là hàm số \(y=-kx+k^2+3\) phải kh.
Đồ thị hàm số đã cho đồng biến trên R khi \(-k>0\Leftrightarrow k< 0\)
Đúng 1
Bình luận (0)
Cho hàm số: y(m-1)x+m (d)a, Tìm m để hàm số đồng biến, nghịch biếnb, Tìm m để hàm số song song với trục hoànhc, Tìm m để đồ thị hàm số đi qua điểm A(-1;1)d, Tìm m để đồ thị hàm số song song với đường thẳng có phương trrình: x-2y1e, Tìm m để đồ thị hàm số cắt trục hoành tại điểm A có hoành độ x2-frac{sqrt{3}}{2}f, Chứng minh rằng đường thẳng (d) luôn đi qua điểm cố định khi m thay đổi
Đọc tiếp
Cho hàm số: y=(m-1)x+m (d)
a, Tìm m để hàm số đồng biến, nghịch biến
b, Tìm m để hàm số song song với trục hoành
c, Tìm m để đồ thị hàm số đi qua điểm A(-1;1)
d, Tìm m để đồ thị hàm số song song với đường thẳng có phương trrình: x-2y=1
e, Tìm m để đồ thị hàm số cắt trục hoành tại điểm A có hoành độ \(x=2-\frac{\sqrt{3}}{2}\)
f, Chứng minh rằng đường thẳng (d) luôn đi qua điểm cố định khi m thay đổi
cho hàm số:
y = mx + 1 (1) (m là tham số)
a) Tìm m để đổ thị hàm số (1) đi qua A(1 ; 4) với giá trị m vừa tìm được hàm số (1) đồng biến hay nghịch biến
b) Tìm m để đô thị hàm số (1) // (d) y = m^2 x X + m + 1
Tìm khoảng đồng biến của hàm số
y
-
x
3
+
3
x
2
-
2
Đọc tiếp
Tìm khoảng đồng biến của hàm số y = - x 3 + 3 x 2 - 2
Cho hàm số
y
f
x
m
2
-
1
x
+
2
m
-
3
.Tất cả các giá trị của tham số m để hàm số đồng biến trên
ℝ
là A.
m
3
2
B. -1 m 1 C.
[
m...
Đọc tiếp
Cho hàm số y = f x = m 2 - 1 x + 2 m - 3 .
Tất cả các giá trị của tham số m để hàm số đồng biến trên ℝ là
A. m > 3 2
B. -1 < m < 1
C. [ m < - 1 m > 1
D. m ≠ ± 1
Hàm số y = ax + b ( a ≠ 0 ) đồng biến trên R khi a> 0.
Do đó, để hàm số đã cho đồng biến trên R thì m 2 - 1 > 0 ⇔ [ m > 1 m < - 1
Chọn C.
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có bảng biến thiên như hình.Hàm số đã cho đồng biến trên khoảng A.
-
∞
;
-
1
B. (-1;3) C. (-3;0) D.
(
0
;
+
∞
)
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên như hình.
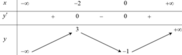
Hàm số đã cho đồng biến trên khoảng
A. - ∞ ; - 1
B. (-1;3)
C. (-3;0)
D. ( 0 ; + ∞ )