Mn ơi, giúp em với. Em cảm ơn ạ!
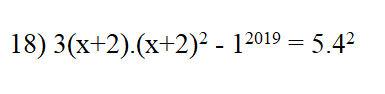
Mn ơi em đang cần gấp ai giúp em với ạ . Em cảm ơn mn nhìu ạ !
Mn ơi, giúp em với. Em cảm ơn ạ!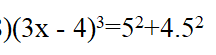
\(\left(3x-4\right)^3=5^2+4.5^2\)
\(\Leftrightarrow\left(3x-4\right)^3=5^2\left(1+4\right)\)
\(\Leftrightarrow\left(3x-4\right)^3=5^3\)
\(\Leftrightarrow3x-4=5\Leftrightarrow3x=9\Leftrightarrow x=3\)
Ta có: \(\left(3x-4\right)^3=5^2+4\cdot5^2\)
\(\Leftrightarrow3x-4=5\)
hay x=3
Mn ơi, giúp em với. Em cảm ơn ạ !

c: \(9^{15}=3^{30}\)
\(27^{10}=3^{30}\)
Do đó: \(9^{15}=27^{10}\)
d: \(2^{333}=8^{111}\)
\(3^{222}=9^{111}\)
Do đó: \(2^{333}< 3^{222}\)
Mn ơi giúp em với. Em cảm ơn ạ!
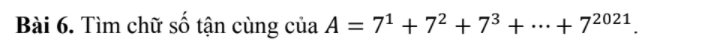
Lời giải:
$A=7+(7^2+7^3+7^4+7^5)+(7^6+7^6+7^8+7^9)+....+(7^{2018}+7^{2019}+7^{2020}+7^{2021})$
$=7+7^2(1+7+7^2+7^3)+7^6(1+7+7^2+7^3)+....+7^{2018}(1+7+7^2+7^3)$
$=7+(1+7+7^2+7^3)(7^2+7^6+....+7^{2018}$
$=7+400(7^2+7^6+....+7^{2018})$
Dễ thấy $400(7^2+7^6+....+7^{2018})$ tận cùng là $0$
Do đó $A$ tận cùng là $7$
Mn ơi, giúp em với. Em cảm ơn ạ!
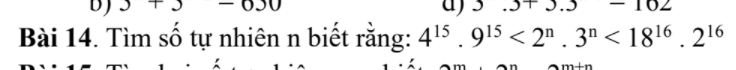
\(4^{15}.9^{15}< 2^n.3^n< 18^{16}.2^{16}\)
⇒\(\left(4.9\right)^{15}< \left(2.3\right)^n< \left(18.2\right)^{16}\)
⇒\(\left(6^2\right)^{15}< 6^n< \left(6^2\right)^{16}\)
⇒\(6^{30}< 6^n< 6^{32}\)
⇒\(6^n=6^{31}\)
⇒n=31
\(4^{15}\cdot9^{15}< 2^n\cdot3^n< 18^{16}\cdot2^{16}\\ \Leftrightarrow\left(4\cdot9\right)^{15}< \left(2\cdot3\right)^n< \left(18\cdot2\right)^{16}\\ \Leftrightarrow36^{15}< 6^n< 36^{16}\\ \Leftrightarrow6^{30}< 6^n< 6^{32}\\ \Leftrightarrow n=31\)
MN ơi giúp em với ạ em cảm ơn

MN ơi giúp em với ạ em cảm ơn
Mn ơi giúp em với ạ:((
Em cảm ơn
 mn ơi giúp em với ạ và giải thích giúp em e cảm ơn mn ❤
mn ơi giúp em với ạ và giải thích giúp em e cảm ơn mn ❤