1. CMR trong một tam giác ta có trực tâm, trọng tâm và giao điểm ba đường trung trực nằm trên một đường thẳng

Những câu hỏi liên quan
Chứng minh rằng trực tâm, trọng tâm và giao điểm của 3 đường trung trực của tam giác cùng nằm trên một đường thẳng.
Cho tam giác ABC, gọi G, H, O lần lượt là trọng tâm, trực tâm và tâm đường tròn ngoại tiếp tam giác ABC. Gọi D là điểm đối xứng của A qua O. Khi đó BHCD là hình bình hành, suy ra trung điểm M của BC cũng là trung điểm của HD. Tam giác AHD có OM là đường trung bình, suy ra OM = ½ AH . Suy ra GM/GA = OM/AH = ½ . Suy ra ΔAHG ∼ ΔMOG (c.g.c)Suy ra H,G, O thẳng hàng và GH = 2GO. Nhận xét. Khi nói đến đường thẳng Euler thì ta chỉ cần cho đường thẳng đi qua hai trong 3 điểm trên.
Đúng 1
Bình luận (0)
Chứng minh rằng trong 1 tam giác, trọng tâm, trực tâm, giao điểm 3 đường trung trực và giao điểm 3 đường phân giác thẳng hàng.
Cho tam giác ABC ( nhọn hoặc tù nhé ) tiếp theo ta vẽ trực tâm của tam giác đó, tiếp nữa ta vẽ trọng tâm của tam giác đó, tiếp đó nữa ta vẽ giao của 3 đường trung trực. Chứng minh rằng trực tâm, trọng tâm và giao của 3 đường trung trực thẳng hàng với nhau.
-Trọng tâm tam giác là giao điểm ba đường trung tuyến
-Trực tâm tam giác là giao điểm bà đường cao kẻ từ 3 đỉnh tam giác
-Giao điểm ba đường trung trực của tam giác là tâm của đường tròn NGOẠI TIẾP
-Giao điểm ba đường phân giác trong của tam giác là tâm đường tròng NỘI TIẾP
Còn các hệ thức trong tam giác vuông mình wên rồi, để bạn nào HS lớp 9 trả
Đúng 1
Bình luận (0)
Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Các điểm A, G, H, I, O phân biệt. Chứng minh rằng:
a) Nếu tam giác ABC cân tại A thì các điểm A, G, H, I, O cùng nằm trên một đường thẳng;
b) Nếu các điểm A, H, I cùng nằm trên một đường thẳng thì tam giác ABC cân tại A.
a)
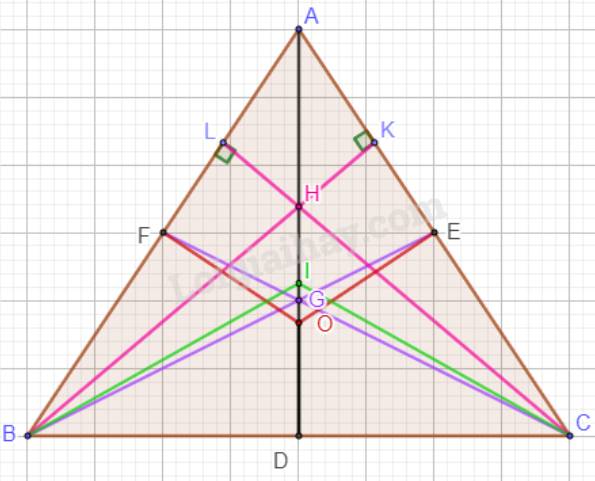
Trong tam giác ABC cân tại A có AD là đường trung tuyến.
Xét tam giác ABD và tam giác ACD có:
AB = AC (tam giác ABC cân);
AD chung;
BD = DC (D là trung điểm của BC).
Vậy \(\Delta ABD = \Delta ACD\)(c.c.c.). Suy ra: \(\widehat {ADB} = \widehat {ADC} = 90^\circ \) (vì ba điểm B, D, C thẳng hàng); \(\widehat {BAD} = \widehat {CAD}\).
Vậy AD là đường cao của tam giác và đường phân giác của góc A.
Suy ra: AD là đường trung trực của tam giác ABC.
Vậy AD là đường trung tuyến, đường cao, đường phân giác, đường trung trực của tam giác ABC.
Mà G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực nên A, G, H, I, O cùng nằm trên một đường thẳng.
Vậy nếu tam giác ABC cân tại A thì các điểm A, G, H, I, O cùng nằm trên một đường thẳng.
b)
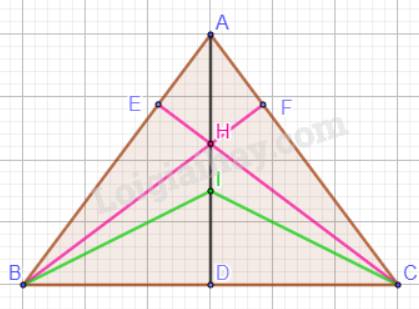
Ta có: \(AD \bot BC\).
H là trực tâm của tam giác ABC nên A, H, D thẳng hàng.
Mà A, H, I thẳng hàng nên A, H, I, K thẳng hàng.
Suy ra: AD là tia phân giác của góc BAC (Vì AI là tia phân giác của góc BAC).
Nên \(\widehat {BAD} = \widehat {CAD}\).
Xét tam giác BAD và tam giác CAD có:
\(\widehat {BAD} = \widehat {CAD}\);
AD chung;
\(\widehat {ADB} = \widehat {ADC}\) (\(AD \bot BC\)).
\(\Rightarrow \Delta ABD = \Delta ACD\)(g.c.g). Suy ra: AB = AC ( 2 cạnh tương ứng).
Do đó, tam giác ABC cân tại A
Vậy nếu các điểm A, H, I cùng nằm trên một đường thẳng thì tam giác ABC cân tại A.
Đúng 0
Bình luận (0)
Câu 1: Xét các khẳng định sau, tìm khẳng định đúng. Trong một tam giác giao điểm của ba trung tuyến gọi là:
A. Trọng tâm tam giác B. Trực tâm tam giác
C. Tâm đường tròn ngoại tiếp tam giác D. Tâm đường tròn nội tiếp tam giác
Câu 2: Cho tam giác ABC có AB AC 10cm, BC 12cm. Vẽ trung tuyến AM của tam giác. Độ dài trung tuyến AM là:
A. 8cm B. √54cm C. √44cm D. 6cm
Câu 3: Cho tam giác ABC, M là tru...
Đọc tiếp
Câu 1: Xét các khẳng định sau, tìm khẳng định đúng. Trong một tam giác giao điểm của ba trung tuyến gọi là: A. Trọng tâm tam giác B. Trực tâm tam giác C. Tâm đường tròn ngoại tiếp tam giác D. Tâm đường tròn nội tiếp tam giác Câu 2: Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Vẽ trung tuyến AM của tam giác. Độ dài trung tuyến AM là: A. 8cm B. √54cm C. √44cm D. 6cm Câu 3: Cho tam giác ABC, M là trung điểm của AC, G là trọng tâm của tam giác ABC và GM = 5cm. Độ dài đoạn BG là: A. 20cm B. 5cm C. 10cm D. 15cm Câu 4: Cho tam giác ABC có AB = AC = 13cm, BC = 10cm. Độ dài đường trung tuyến AM là: A. 12cm B. 10cm C. 8cm D. 6cm Câu 5: Trong một tam giác, điểm cách đều ba cạnh là: A. Giao điểm ba đường trung tuyến B. Giao điểm của ba đường trung trực C. Giao điểm ba đường phân giác D. Giao điểm ba đường cao Câu 6: Nếu một tam giác có một đường trung tuyến đồng thời là đường cao thì tam giác đó là: A. Tam giác vuông B. Tam nhọn C. Tam giác cân D. Tam giác tù Câu 7: Cho tam giác ABC, M là trung điểm của BC, G là trọng tâm của tam giác ABC và AM=18cm. Độ dài đoạn AG là: A. 12cm B. 6cm C. 9cm D. 10cm Câu 8: Cho tam giác ABC cân tại A, các đường trung tuyến BC và CE cắt nhau tại G. Chọn khẳng định đúng trong các khẳng định sau: A. AG là tia phân giác của góc A của tam giác ABC B. AG là đường trung trực của BC của tam giác ABC C. AG là đường cao của tam giác ABC D. Cả ba khẳng định đều đúng Câu 9: Cho tam giác ABC cân tại A, BC = 10cm. Độ dài đường trung tuyến AM bằng 12cm. Khi đó độ dài AB là A. 12cm B. 13cm C. 11cm D. 10cm Câu 10: Cho tam giác ABC vuông tại A. Trực tâm của tam giác ABC là điểm A. Nằm bên trong tam giác B. Nằm bên ngoài tam giác C. Là trung điểm của cạnh huyền BC D. Trùng với điểm A Câu 11: Đường trung trực của cạnh BC trong tam giác ABC cắt cạnh AC tại D. Cho AC = 10cm, BD = 4cm. Khi đó AD là: A. 6cm B. 4cm C. 3cm D. 5cm
Câu 1: B
Câu 2: C
Câu 3: C
Câu 4: A
Câu 5: D
Câu 6: B
Câu 7: C
Câu 8: D
Đúng 0
Bình luận (1)
Câu 1: Xét các khẳng định sau, tìm khẳng định đúng.
Trong một tam giác giao điểm của ba trung tuyến gọi là:
A. Trọng tâm tam giác
Câu 2: Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Vẽ trung tuyến AM của tam giác. Độ dài trung tuyến AM là:
A. 8cm
Câu 3: Cho tam giác ABC, M là trung điểm của AC, G là trọng tâm của tam giác ABC và GM = 5cm. Độ dài đoạn BG là:
D. 15cm
Câu 4: Cho tam giác ABC có AB = AC = 13cm, BC = 10cm. Độ dài đường trung tuyến AM là:
A. 12cm
Câu 5: Trong một tam giác, điểm cách đều ba cạnh là:
C. Giao điểm ba đường phân giác
Câu 6: Nếu một tam giác có một đường trung tuyến đồng thời là đường cao thì tam giác đó là:
C. Tam giác cân
Câu 7: Cho tam giác ABC, M là trung điểm của BC, G là trọng tâm của tam giác ABC và AM=18cm. Độ dài đoạn AG là:
B. 6cm
Đúng 0
Bình luận (1)
Xét các khẳng định sau, tìm khẳng định đúng. Trong một tam giác giao điểm của ba trung tuyến gọi là:
A. Trọng tâm tam giác
B. Trực tâm tam giác
C. Tâm đường tròn ngoại tiếp tam giác
D. Tâm đường tròn nội tiếp tam giác
Xem thêm câu trả lời
Câu 1: Xét các khẳng định sau, tìm khẳng định đúng. Trong một tam giác giao điểm của ba trung tuyến gọi là:
A. Trọng tâm tam giác
B. Trực tâm tam giác
C. Tâm đường tròn ngoại tiếp tam giác
D. Tâm đường tròn nội tiếp tam giác
Câu 2: Cho tam giác ABC có AB AC 10cm, BC 12cm. Vẽ trung tuyến AM của tam giác. Độ dài trung tuyến AM là:
A. 8cm
B. √54cm
C. √44cm
D. 6cm
Câu 3: Cho tam giác ABC,...
Đọc tiếp
Câu 1: Xét các khẳng định sau, tìm khẳng định đúng. Trong một tam giác giao điểm của ba trung tuyến gọi là: A. Trọng tâm tam giác B. Trực tâm tam giác C. Tâm đường tròn ngoại tiếp tam giác D. Tâm đường tròn nội tiếp tam giác Câu 2: Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Vẽ trung tuyến AM của tam giác. Độ dài trung tuyến AM là: A. 8cm B. √54cm C. √44cm D. 6cm Câu 3: Cho tam giác ABC, M là trung điểm của AC, G là trọng tâm của tam giác ABC và GM = 5cm. Độ dài đoạn BG là: A. 20cm B. 5cm C. 10cm D. 15cm Câu 4: Cho tam giác ABC có AB = AC = 13cm, BC = 10cm. Độ dài đường trung tuyến AM là: A. 12cm B. 10cm C. 8cm D. 6cm Câu 5: Trong một tam giác, điểm cách đều ba cạnh là: A. Giao điểm ba đường trung tuyến B. Giao điểm của ba đường trung trực C. Giao điểm ba đường phân giác D. Giao điểm ba đường cao Câu 6: Nếu một tam giác có một đường trung tuyến đồng thời là đường cao thì tam giác đó là: A. Tam giác vuông B. Tam nhọn C. Tam giác cân D. Tam giác tù Câu 7: Cho tam giác ABC, M là trung điểm của BC, G là trọng tâm của tam giác ABC và AM=18cm. Độ dài đoạn AG là: A. 12cm B. 6cm C. 9cm D. 10cm Câu 8: Cho tam giác ABC cân tại A, các đường trung tuyến BC và CE cắt nhau tại G. Chọn khẳng định đúng trong các khẳng định sau: A. AG là tia phân giác của góc A của tam giác ABC B. AG là đường trung trực của BC của tam giác ABC C. AG là đường cao của tam giác ABC D. Cả ba khẳng định đều đúng Câu 9: Cho tam giác ABC cân tại A, BC = 10cm. Độ dài đường trung tuyến AM bằng 12cm. Khi đó độ dài AB là A. 12cm B. 13cm C. 11cm D. 10cm Câu 10: Cho tam giác ABC vuông tại A. Trực tâm của tam giác ABC là điểm A. Nằm bên trong tam giác B. Nằm bên ngoài tam giác C. Là trung điểm của cạnh huyền BC D. Trùng với điểm A Câu 11: Đường trung trực của cạnh BC trong tam giác ABC cắt cạnh AC tại D. Cho AC = 10cm, BD = 4cm. Khi đó AD là: A. 6cm B. 4cm C. 3cm D. 5cm
Cho tam giác ABC có 3 đỉnh nằm trên một đường tròn O. Vẽ trực tâm H và trọng tâm G của tam giác. Kẻ đường cao AD. Giao điểm thứ hai của AD với đường tròn tâm O là E. Kẻ đường kính AP. Biết góc BAE bằng Góc BCE.
CMR 1, DH=DE
2, Tứ giác BPCH là hình bình hành
3, G nằm giữa OH, GH và GH = 2 GO
Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Chứng minh rằng:
a) Nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau;
b) Nếu tam giác ABC có hai điểm trong bốn điểm G, H, I, O trùng nhau thì tam giác ABC là tam giác đều.
a)
Ta có:
G là trọng tâm của tam giác ABC (giao điểm của ba đường trung tuyến);
H là trực tâm của tam giác ABC (giao điểm của ba đường cao);
I là giao điểm của ba đường phân giác của tam giác ABC;
O là giao điểm của ba đường trung trực của tam giác ABC (Đường trung trực đi qua trung điểm của cạnh và vuông góc với cạnh tại trung điểm đó).
Mà tam giác ABC đều nên trong tam giác ABC đường trung tuyến đồng thời là đường cao và là đường phân giác.
Vậy bốn điểm G, H, I, O trùng nhau hay nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau.
b)
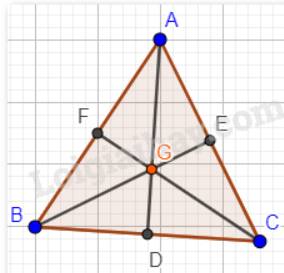
Giả sử trong tam giác ABC có hai điểm trùng nhau là H (trực tâm của tam giác) và I (giao của ba đường phân giác).
Hay AD, BE, CF vừa là đường cao, vừa là đường phân giác của tam giác ABC.
Xét tam giác ADB và tam giác ADC có:
\(\widehat {BAD} = \widehat {CAD}\) ( vì AD là tia phân giác của góc BAC)
AD chung;
\(\widehat {ADB} = \widehat {ADC}(=90^0)\) (vì \(AD \bot BC\));
Vậy \(\Delta ADB = \Delta ADC\)(g.c.g). Suy ra: AB = AC( 2 cạnh tương ứng). (1)
Tương tự ta có: \(\Delta AEB = \Delta CEB\)(c.g.c). Suy ra: AB = BC ( 2 cạnh tương ứng). (2)
Từ (1) và (2) suy ra: AB = BC = AC.
Vậy tam giác ABC đều hay nếu tam giác ABC có hai điểm trong bốn điểm G, H, I, O trùng nhau thì tam giác ABC là tam giác đều.
Đúng 0
Bình luận (0)





















