Cho góc vuông xOy cố định, Lấy A,B cố định trên tia Ox, C di động trên tia Oy. Đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BC tại B cắt nhau tại M. Các điểm M nằm trên đường nào?

Những câu hỏi liên quan
Cho góc xOy cố định khác góc bẹt. Các điểm A và B theo thứ tự chuyển động trên các tia Ox và Oy sao cho OA = OB. Đường vuông góc với OA tại A và đường vuông góc với OB tại B cắt nhau ở M. Điểm M chuyển động trên đường nào ?
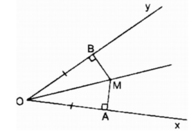
Xét hai tam giác vuông MOA và MOB: ∠ (MAO) = ∠ (MBO) = 90 0
OA = OB (gt)
OM cạnh huyền chung
Do đó: ∆ MAO = ∆ MBO (cạnh huyền, cạnh góc vuông)
⇒ ∠ (AOM) = ∠ (BOM)
A và B thay đổi, OA và OB luôn bằng nhau nên ∆ MAO và ∆ MBO luôn luôn bằng nhau do đó ∠ (AOM) = ∠ (BOM)
Vậy khi A chuyển động trên Ox, B chuyển động trên Oy mà OA = OB thì điểm M chuyển động trên tia phân giác của góc xOy.
Đúng 0
Bình luận (0)
Cho góc vuông xOy. Lấy các điểm I và K lần lượt trên các tia Ox và Oy. Đường tròn (I; OK) cắt tia Ox tại M (I nằm giữa O và M), đường tròn (K; OI) cắt tia Oy tại N (K nằm giữa O và N)a, Chứng minh (I) và (K) luôn cắt nhaub, Tiếp tuyến tại M của (I), tiếp tuyến tại N của đường tròn (K) cắt nhau tại C. Chứng minh tứ giác OMCN là hình vuôngc, Gọi A, B là các giao điểm của (I) và (K) trong đó B ở miền trong góc xOy. Chứng minh ba điểm A, B, C thẳng hàngd, Giả sử I và K thứ tự di động trên các tia Ox...
Đọc tiếp
Cho góc vuông xOy. Lấy các điểm I và K lần lượt trên các tia Ox và Oy. Đường tròn (I; OK) cắt tia Ox tại M (I nằm giữa O và M), đường tròn (K; OI) cắt tia Oy tại N (K nằm giữa O và N)
a, Chứng minh (I) và (K) luôn cắt nhau
b, Tiếp tuyến tại M của (I), tiếp tuyến tại N của đường tròn (K) cắt nhau tại C. Chứng minh tứ giác OMCN là hình vuông
c, Gọi A, B là các giao điểm của (I) và (K) trong đó B ở miền trong góc xOy. Chứng minh ba điểm A, B, C thẳng hàng
d, Giả sử I và K thứ tự di động trên các tia Ox và Oy sao cho OI + OK = a không đổi. Chứng minh đường thẳng AB luôn đi qua một điểm cố định

a, Chỉ ra |OI – OK| < IK < OI + OK => (1) và (k) luôn cắt nhau
b, Do OI=NK, OK=IM => OM=ON
Mặt khác OMCN là hình chữ nhật => OMCN là hình vuông
c, Gọi{L} = KB ∩ MC, {P} = IBNC => OKBI là Hình chữ nhật và BNMI là hình vuông
=> ∆BLC = ∆KOI
=> L B C ^ = O K I ^ = B I K ^
mà B I K ^ + I B A ^ = 90 0
L B C ^ + L B I ^ + I B A ^ = 180 0
d, Có OMCN là hình vuông cạnh a cố định
=> C cố định và AB luôn đi qua điểm C
Đúng 0
Bình luận (0)
Cho góc xOy cố định khác góc bẹt. Các điểm A và B theo thứ tự chuyển động trên các tia Ox và Oy sao cho OA = OB. Đường vuông góc với OB tại B cắt nhau ở M. Điểm M chuyển động trên đường nào ?
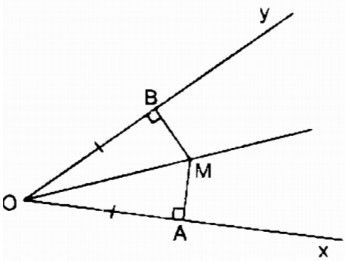
Xét hai tam giác vuông MOA và MOB:
\(\widehat{MAO}=\widehat{MBO}=90^0\)
OA = OB (gt)
OM cạnh huyền chung
Do đó: ∆ MAO = ∆ MBO (cạnh huyền, cạnh góc vuông)
⇒\(\widehat{AOM}=\widehat{BOM}\)
A và B thay đổi, OA và OB luôn bằng nhau nên ∆ MAO và ∆ MBO luôn luôn bằng nhau do đó \(\widehat{AOM}=\widehat{BOM}\)
Vậy khi A chuyển động trên Ox, B chuyển động trên Oy mà OA = OB thì điểm M chuyển động trên tia phân giác của góc xOy.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A (ABAC). Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BDCE. Đường thẳng vuông góc với BC tại D cắt AB tại M, đường thẳng vuông góc với BC tại E cắt AC tại N.a)CMR: DMENb)CMR đường thẳng BC cắt đoạn MN tại trung điểm I của nóc)CMR đường thẳng vuông góc với MN tại I luôn đi qua 1 điểm cố định khi D di động trên cạnh BC
Đọc tiếp
Cho tam giác ABC cân tại A (AB=AC). Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE. Đường thẳng vuông góc với BC tại D cắt AB tại M, đường thẳng vuông góc với BC tại E cắt AC tại N.
a)CMR: DM=EN
b)CMR đường thẳng BC cắt đoạn MN tại trung điểm I của nó
c)CMR đường thẳng vuông góc với MN tại I luôn đi qua 1 điểm cố định khi D di động trên cạnh BC
Câu hỏi của Nguyễn Thành Nam - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại link trên nhé.
Đúng 0
Bình luận (0)
Cho góc nhọn xOy , trên tia Ox lấy điểm A , trên tia Oy lấy điểm B . Từ A kẻ đường thẳng vuông góc với Ox , cắt Oy tại C . Từ B kẻ đường thẳng vuông góc với Oy , cắt Ox tại D .CMR: AC=BD
Không thể bằng nhau được bạn ạ mà chỉ xảy ra TH đồng dạng vì đâu có cặp cạnh nào bằng nhau cho trước sẵn đâu
\(\hept{\begin{cases}OA\ne OB\\OD\ne OC\end{cases}}\)
Đúng 0
Bình luận (0)
Mik nghĩ cần bổ sung thêm OB=OA.
Xét tam giác OAC và OBD có:OA=OB,^OBD=^OAC,^AOB chung
Khi đó \(\Delta\)OAC=\(\Delta\)OBD ( ch-gn ) => AC=BD
Đúng 1
Bình luận (0)
Sửa hộ mik tí.trường hợp cạnh góc vuông và góc nhọn kề cạnh ấy nha !Hình mình hay nhầm lẫn lắm:((
Đúng 0
Bình luận (0)
Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B. Từ A kẻ đường thẳng vuông góc với Ox, cắt Oy tại C. Từ B kẻ đường thẳng vuông góc với Oy, cắt Ox tại D. CMR: AC = BD
Nhớ vẽ hình nha!!
Cho góc vuông xOY cố định. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B, hai điểm A và B chuyển động sao cho OA+OB = a (a không đổi). Vẽ 2 đường tròn (A;OB); (B;OA), chúng cắt nhau tại D và E. Cm đường thẳng DE luôn đi qua 1 điểm cố định
Cho góc xOy nhọn . Trên cạnh Ox , lấy A và trên Oy lấy B sao cho OA OB. Từ A kẻ AC vuông góc với Oy tại C , từ B kẻ BD vuông góc với Ox tại D , AC và BD cắt nhau tại N . Đường thẳng vuông góc với Ox kẻ từ A cắt đường thẳng vuông góc với Oy kẻ từ B tại M .a. Chứng minh : N nằm trên tia phân giác của góc xOyb. Chứng minh : O , M , N thẳng hàngc. Chứng minh : OM vuông góc với AB để suy ra AB song song với CDGiúp với câu BC mai cần gấp ai làm dc thì dc tick nhiều học giỏi
Đọc tiếp
Cho góc xOy nhọn . Trên cạnh Ox , lấy A và trên Oy lấy B sao cho OA = OB. Từ A kẻ AC vuông góc với Oy tại C , từ B kẻ BD vuông góc với Ox tại D , AC và BD cắt nhau tại N . Đường thẳng vuông góc với Ox kẻ từ A cắt đường thẳng vuông góc với Oy kẻ từ B tại M .
a. Chứng minh : N nằm trên tia phân giác của góc xOy
b. Chứng minh : O , M , N thẳng hàng
c. Chứng minh : OM vuông góc với AB để suy ra AB song song với CD
Giúp với câu BC mai cần gấp ai làm dc thì dc tick nhiều học giỏi
Cho △ABC cân tại A. Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD CE. Đường thẳng vuông góc với BC tại D cắt AB tại M, đường thẳng vuông góc với BC tại E cắt đường thẳng AC tại N. MN cắt BC tại I.C/Ma)DMEM (có thể bỏ qua)b)IMIN;BCMNc)gọi O là giao điểm của đường phân giác góc A và đường vuông góc MN tại I. C/m tam giác BNO tam giác CNO.Từ đó suy ra điểm O cố định
Đọc tiếp
Cho △ABC cân tại A. Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Đường thẳng vuông góc với BC tại D cắt AB tại M, đường thẳng vuông góc với BC tại E cắt đường thẳng AC tại N. MN cắt BC tại I.C/M
a)DM=EM (có thể bỏ qua)
b)IM=IN;BC<MN
c)gọi O là giao điểm của đường phân giác góc A và đường vuông góc MN tại I. C/m tam giác BNO= tam giác CNO.Từ đó suy ra điểm O cố định
Bn tham khảo ở đây nha : https://olm.vn/hoi-dap/detail/86073517597.html
Đúng 0
Bình luận (0)
Hình này đẹp hơn :D.Mà mình không hiểu câu b lắm,nên ghi rõ hơn là IM = IN > BC và c/m MN > BC hay sao? ghi hai dấu vậy khó hiểu lắm.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Từ A kẻ đường thẳng vuông góc với Ox cắt Oy tại M, từ B kẻ đường thẳng vuông góc với Oy cắt Ox tại N. AM cắt BN tại K. Chứng minh:
a) \(\Delta AKN\) = \(\Delta BKM\)
b) OK là phân giác của góc AOB
a: Xét ΔOAM vuông tại A và ΔOBN vuông tại B có
OA=OB
\(\widehat{AOB}\) chung
Do đó: ΔOAM=ΔOBN
=>\(\widehat{OMA}=\widehat{ONB}\) và OM=ON
Ta có: OA+AN=ON
OB+BM=OM
mà OA=OB và ON=OM
nên AN=BM
Xét ΔKAN vuông tại A và ΔKBM vuông tại B có
KA=KB
\(\widehat{KNA}=\widehat{KMB}\)
Do đó: ΔKAN=ΔKBM
b: ΔKAN=ΔKBM
=>KA=KB
Xét ΔOAK vuông tại A và ΔOBK vuông tại B có
OK chung
OA=OB
Do đó: ΔOAK=ΔOBK
=>\(\widehat{AOK}=\widehat{BOK}\)
=>OK là phân giác của \(\widehat{AOB}\)
Đúng 2
Bình luận (1)




















