Giải phương trình
-x3 + 2x +7 = 0
Giải phương trình bằng cách đưa về phương trình tích:
x3 + 3x2 – 2x – 6 = 0
x3 + 3x2 – 2x – 6 = 0
⇔ (x3 + 3x2) – (2x + 6) = 0
⇔ x2(x + 3) – 2(x + 3) = 0
⇔ (x2 – 2)(x + 3) = 0
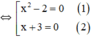
+ Giải (1): x2 – 2 = 0 ⇔ x2 = 2 ⇔ x = √2 hoặc x = -√2.
+ Giải (2): x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm S = {-3; -√2; √2}
Giải phương trình sau bằng cách đưa về phương trình tích: x3 + 3x2 + 2x = 0.
x3 + 3x2 + 2x = 0 ⇔ x(x2 + 3x + 2) = 0
⇔ x = 0 hoặc x2 + 3x + 2 = 0 (1)
Giải phương trình (1) ta được các nghiệm x = -1; x = -2
Vậy phương trình đã cho có 3 nghiệm x = 0; x = -1; x = -2
Giải phương trình sau bằng cách đưa về phương trình tích: x 3 + 3 x 2 + 2 x = 0 .
x 3 + 3 x 2 + 2 x = 0 ⇔ x ( x 2 + 3 x + 2 ) = 0
⇔ x = 0 hoặc x 2 + 3 x + 2 = 0 ( 1 )
Giải phương trình (1) ta được các nghiệm x = -1; x = -2
Vậy phương trình đã cho có 3 nghiệm x = 0; x = -1; x = -2
Giải các phương trình sau:
a) 7 − x 2 4 − x + 5 2 = 0 ;
b) 4 x 2 + x − 1 2 − 2 x + 1 2 = 0 ;
c) x 3 + 1 = x + 1 2 − x ;
d) x 2 − 4 x − 5 = 0 .
Giải các phương trình: x 4 - 2 x 3 + 3 x 2 - 2x + 3 = 0
Bài 6: Giải các phương trình sau:
2) |
3) |
4) |
5) |
6) |
7) |
8)
9)
10)
11)
12)
13)
14) x2 – 2x + 1 = 0
15) 1 + 3x + 3x2 + x3 = 0
4) Ta có: \(\dfrac{2x-5}{5}-\dfrac{x+3}{3}=\dfrac{2-3x}{2}-x-2\)
\(\Leftrightarrow\dfrac{6\left(2x-5\right)}{30}-\dfrac{10\left(x+3\right)}{30}=\dfrac{15\left(2-3x\right)}{30}-\dfrac{30\left(x+2\right)}{30}\)
\(\Leftrightarrow12x-30-10x-30=30-45x-30x-60\)
\(\Leftrightarrow-22x-60=-75x-30\)
\(\Leftrightarrow-22x+75x=-30+60\)
\(\Leftrightarrow53x=30\)
\(\Leftrightarrow x=\dfrac{30}{53}\)
Vậy: \(S=\left\{\dfrac{30}{53}\right\}\)
5) Ta có: \(\dfrac{5x-3}{6}-\dfrac{7x-1}{4}=5\)
\(\Leftrightarrow\dfrac{2\left(5x-3\right)}{12}-\dfrac{3\left(7x-1\right)}{12}=\dfrac{60}{12}\)
\(\Leftrightarrow10x-6-21x+3=60\)
\(\Leftrightarrow-11x-3=60\)
\(\Leftrightarrow-11x=63\)
\(\Leftrightarrow x=-\dfrac{63}{11}\)
Vậy: \(S=\left\{-\dfrac{63}{11}\right\}\)
`9,x^3+x^2-2=0`
`x^3-x^2+2x^2-2=0`
`<=>x^2(x-1)+2(x-1)(x+1)=0`
`<=>(x-1)(x^2+2x+2)=0`
`<=>x=1`
`14,x^2-2x+1=0`
`<=>(x-1)^2=0`
`<=>x-1=0`
`<=>x=1`
`15,x^3+3x^2+3x+1=0`
`<=>(x+1)^3=0`
`<=>x+1=0`
`<=>x=-1`
Bài 6: Giải các phương trình sau:
1) |
2) |
3) |
4) |
5) |
6) |
7) |
8)
9)
10)
11)
12)
13)
14) x2 – 2x + 1 = 0
15) 1 + 3x + 3x2 + x3 = 0
Bài 6:
1) Ta có: \(2x\left(x-5\right)-\left(x+3\right)^2=3x-x\left(5-x\right)\)
\(\Leftrightarrow2x^2-10x-\left(x^2+6x+9\right)=3x-5x+x^2\)
\(\Leftrightarrow2x^2-10x-x^2-6x-9-3x+5x-x^2=0\)
\(\Leftrightarrow-14x-9=0\)
\(\Leftrightarrow-14x=9\)
\(\Leftrightarrow x=-\dfrac{9}{14}\)
Vậy: \(S=\left\{-\dfrac{9}{14}\right\}\)
`1)2x(x-5)-(x+3)^2=3x-x(5-x)`
`<=>2x^2-10x-x^2-6x-9=3x-5x+x^2`
`<=>x^2-16x-9=x^2-2x`
`<=>14x=-9`
`<=>x=-9/14`
Giải các phương trình sau:
a) x x − 3 + 2 x − 3 = 0 ;
b) x 2 x − 1 − x 2 x + 2 + x 3 − x + 3 = 0
a) Biến đổi về dạng (x - 3)(x + 2) = 0. Tìm được x ∈ { - 2 ; 3 }
b) Thu gọn về dạng -2x + 3 = 0. Tìm được x = 3 2
Giải các phương trình sau:
a) x − 1 2 − 2 x + 5 2 = 0 ;
b) x 2 − 1 − x 2 − 2 x − 1 2 = 0 ;
c) x 3 + 8 = − 2 x x + 2 ;
d) 4 x 2 + 8 x − 5 = 0 .
từ dễ đến bình thường
giải các phương trình sau
1)3=x-8
2)2x=7+x
3)x-(8-x)=4
1. 3=x-8
\(\Leftrightarrow\)x=11
Vậy ...
2. 2x=7+x
\(\Leftrightarrow\)2x-x=7
\(\Leftrightarrow\)x(2-1)=7
\(\Leftrightarrow\)x=7
Vậy ...
3. x-(8-x)=4
\(\Leftrightarrow\)x-8+x=4
\(\Leftrightarrow\)2x-8=4
\(\Leftrightarrow\)2x=12
\(\Leftrightarrow\)x=6
Vậy ...
1) \(3=x-8\)
\(\Leftrightarrow x=11\).
-Vậy \(S=\left\{11\right\}\).
2) \(2x=7+x\)
\(\Leftrightarrow x-7=0\)
\(\Leftrightarrow x=7\).
-Vậy \(S=\left\{7\right\}\).
3) \(x-\left(8-x\right)=4\)
\(\Leftrightarrow2x-8-4=0\)
\(\Leftrightarrow2x-12=0\)
\(\Leftrightarrow x=6\)
-Vậy \(S=\left\{6\right\}\)