Giúp em câu d ạ

Những câu hỏi liên quan
Giúp em với và cảm ơn ạ. Em cần giúp câu b, c, d ạ
Mn giúp em câu b,c,d ạ, em cần gấp ạ
a) Thay \(x=\dfrac{1}{4}\) vào Q, ta được:
\(Q=\dfrac{1}{\dfrac{1}{4}\cdot\dfrac{1}{2}+27}=\dfrac{1}{27+\dfrac{1}{8}}=\dfrac{8}{217}\)
b) Ta có: \(P=\dfrac{x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}-\dfrac{1}{2-\sqrt{x}}-\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
\(=\dfrac{x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}+3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-9+\sqrt{x}+3-x+2\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3\sqrt{x}-6}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3}{\sqrt{x}+3}\)
c) Để \(P>\dfrac{1}{2}\) thì \(P-\dfrac{1}{2}>0\)
\(\Leftrightarrow\dfrac{6-\left(\sqrt{x}+3\right)}{2\left(\sqrt{x}+3\right)}>0\)
\(\Leftrightarrow3-\sqrt{x}>0\)
\(\Leftrightarrow x< 9\)
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0\le x< 9\\x\ne4\end{matrix}\right.\)
Đúng 3
Bình luận (0)
Ac nào giúp em câu 3 được không ạ em biết là câu D nhưng không biết sửa như nào ạ ????
Giúp em câu b với câu d với ạ.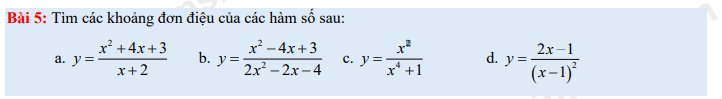
 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB, ta được:
\(AM\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC, ta được:
\(AN\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
Đúng 0
Bình luận (0)
Giúp em câu d ạ 
d) Xét tứ giác ACBK có
\(\widehat{CAB}=\widehat{CKB}\left(=90^0\right)\)
nên ACBK là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Suy ra: \(\widehat{DAK}=\widehat{DCB}\)(hai góc nội tiếp cùng chắn cung KB)
Xét ΔADK và ΔCDB có
\(\widehat{DAK}=\widehat{DCB}\)(cmt)
\(\widehat{ADK}=\widehat{CDB}\)(hai góc đối đỉnh)
Do đó: ΔADK\(\sim\)ΔCDB(g-g)
Đúng 0
Bình luận (0)
giúp em câu d ạ ;-;
giúp em bài 1 câu c câu d với ạ!!!

`D=(sqrt{3}.sqrt{5-2sqrt6})/(sqrt3-sqrt2)-1/(2-sqrt3)`
`=(sqrt3*sqrt{3-2sqrt{3}.sqrt2+2})/(sqrt3-sqrt2)-(2+sqrt3)/(4-3)`
`=(sqrt3.sqrt{(sqrt3-sqrt2)^2})/(sqrt3-sqrt2)-2-sqrt3`
`=sqrt3-2-sqrt3=-2`
Đúng 1
Bình luận (3)
c) Ta có: \(C=\sqrt{\dfrac{3\sqrt{5}+1}{2\sqrt{5}-3}}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{\left(3\sqrt{5}+1\right)\left(2\sqrt{5}-3\right)}}{2\sqrt{5}-3}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{30-9\sqrt{5}+2\sqrt{5}-3}}{2\sqrt{5}-3}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{27-7\sqrt{5}}}{2\sqrt{5}-3}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{54-14\sqrt{5}}}{2\sqrt{10}-3\sqrt{2}}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\left(7-\sqrt{5}\right)\cdot\sqrt{2}\left(\sqrt{5}-1\right)}{\sqrt{2}\cdot\left(2\sqrt{5}-3\right)}\)
\(=\dfrac{7\sqrt{5}-7-5+\sqrt{5}}{2\sqrt{5}-3}\)
\(=\dfrac{8\sqrt{5}-12}{2\sqrt{5}-3}\)
\(=\dfrac{4\left(2\sqrt{5}-3\right)}{2\sqrt{5}-3}=4\)
Đúng 0
Bình luận (0)













