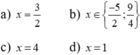x/x-1- 2x/x2-1=0

Những câu hỏi liên quan
1 Trong các phương trình sau, phương trình nào vô nghiệm:
A. x2 – 2x + 2 = 0 B. x2 – 2x + 1 = 0
C. x2 – 2x = 0 D. 2x – 10 = 2x – 10
2 Phương trình nào sau đây có 1 nghiệm :
A. x2 – 3 x = 0 B. 2x + 1 =1 +2x
C. x ( x – 1 ) = 0 D. (x + 2)(x2 + 1) = 0
a) x2(x - 5) + 5 - x = 0; b) 3x4 - 9x3 = -9x2 + 27x;
c) x2(x + 8) + x2 = -8x; d) (x + 3)(x2 -3x + 5) = x2 + 3x.
e) 3x(x - 1) + x - 1 = 0;
f) (x - 2)(x2 + 2x + 7) + 2(x2 - 4) - 5(x - 2) = 0;
g) (2x - 1)2 - 25 = 0;
h) x3 + 27 + (x + 3)(x - 9) = 0.
i)8x3 - 50x = 0; k) 2(x + 3)-x2 - 3x = 0;
m)6x2 - 15x - (2x - 5)(2x + 5) =
a: \(\Leftrightarrow\left(x-5\right)\left(x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\\x=1\end{matrix}\right.\)
d: \(\Leftrightarrow\left(x+3\right)\left(x^2-4x+5\right)=0\)
\(\Leftrightarrow x+3=0\)
hay x=-3
Đúng 0
Bình luận (0)
Bài 11: Tìm x biết:
a) (x+2)(x2-2x+4) - x(x2+2) =15
b) (x+3)2 –x(3x+1)2 +(2x+1)(4x2 -2x+1) =28
c) (x2-1)3 - (x4+x2+1)(x2-1) = 0
d) (x-2)3 –(x-3)(x2 + 3x+9) +6(x+1)2 = 49
Giải các phương trình tích sau:1.a)(3x – 2)(4x + 5) 0 b) (2,3x – 6,9)(0,1x + 2) 0c)(4x + 2)(x2 + 1) 0 d) (2x + 7)(x – 5)(5x + 1) 02. a)(3x + 2)(x2 – 1) (9x2 – 4)(x + 1) b)x(x + 3)(x – 3) – (x + 2)(x2 – 2x + 4) 0c)2x(x – 3) + 5(x – 3) 0 d)(3x – 1)(x2 + 2) (3x – 1)(7x – 10)3.a)(2x – 5)2 – (x + 2)2 0 b)(3x2 + 10x – 8)2 (5x2 – 2x + 10)2c)(x2 – 2x + 1) – 4 0 d)4x2 + 4x + 1 x24. a) 3x2 + 2x – 1 0 b) x2 – 5x + 6 0c) x2 – 3x + 2 0 d) 2x2 – 6x + 1 0 ...
Đọc tiếp
Giải các phương trình tích sau:
1.a)(3x – 2)(4x + 5) = 0 b) (2,3x – 6,9)(0,1x + 2) = 0
c)(4x + 2)(x2 + 1) = 0 d) (2x + 7)(x – 5)(5x + 1) = 0
2. a)(3x + 2)(x2 – 1) = (9x2 – 4)(x + 1)
b)x(x + 3)(x – 3) – (x + 2)(x2 – 2x + 4) = 0
c)2x(x – 3) + 5(x – 3) = 0 d)(3x – 1)(x2 + 2) = (3x – 1)(7x – 10)
3.a)(2x – 5)2 – (x + 2)2 = 0 b)(3x2 + 10x – 8)2 = (5x2 – 2x + 10)2
c)(x2 – 2x + 1) – 4 = 0 d)4x2 + 4x + 1 = x2
4. a) 3x2 + 2x – 1 = 0 b) x2 – 5x + 6 = 0
c) x2 – 3x + 2 = 0 d) 2x2 – 6x + 1 = 0
e) 4x2 – 12x + 5 = 0 f) 2x2 + 5x + 3 = 0
Bài 1:
a) (3x - 2)(4x + 5) = 0
<=> 3x - 2 = 0 hoặc 4x + 5 = 0
<=> 3x = 2 hoặc 4x = -5
<=> x = 2/3 hoặc x = -5/4
b) (2,3x - 6,9)(0,1x + 2) = 0
<=> 2,3x - 6,9 = 0 hoặc 0,1x + 2 = 0
<=> 2,3x = 6,9 hoặc 0,1x = -2
<=> x = 3 hoặc x = -20
c) (4x + 2)(x^2 + 1) = 0
<=> 4x + 2 = 0 hoặc x^2 + 1 # 0
<=> 4x = -2
<=> x = -2/4 = -1/2
d) (2x + 7)(x - 5)(5x + 1) = 0
<=> 2x + 7 = 0 hoặc x - 5 = 0 hoặc 5x + 1 = 0
<=> 2x = -7 hoặc x = 5 hoặc 5x = -1
<=> x = -7/2 hoặc x = 5 hoặc x = -1/5
bài 2:
a, (3x+2)(x^2-1)=(9x^2-4)(x+1)
(3x+2)(x-1)(x+1)=(3x-2)(3x+2)(x+1)
(3x+2)(x-1)(x+1)-(3x-2)(3x+2)(x+1)=0
(3x+2)(x+1)(1-2x)=0
b, x(x+3)(x-3)-(x-2)(x^2-2x+4)=0
x(x^2-9)-(x^3+8)=0
x^3-9x-x^3-8=0
-9x-8=0
tự tìm x nha
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
2
x
−
1
2
x
−
5
;
b)
7
−
x
−
2
−
3
x
0
;
c)...
Đọc tiếp
Giải các phương trình sau:
a) 2 x − 1 = 2 x − 5 ; b) 7 − x − 2 − 3 x = 0 ;
c) x − 4 + x 2 − 5 x + 4 = 0 ; d) x 2 − x − 2 x + 1 − x = 0 .
Tìm x, biết:a) 3x(x - 1) + x - 1 0;b) (x - 2)(
x
2
+ 2x + 7) + 2(
x
2
- 4) - 5(x - 2) 0;c)
(
2
x
-
1
)
2
- 25 0;d)
x
3
+ 27 + (x + 3)(x - 9) 0.
Đọc tiếp
Tìm x, biết:
a) 3x(x - 1) + x - 1 = 0;
b) (x - 2)( x 2 + 2x + 7) + 2( x 2 - 4) - 5(x - 2) = 0;
c) ( 2 x - 1 ) 2 - 25 = 0;
d) x 3 + 27 + (x + 3)(x - 9) = 0.
a) x = 1; x = - 1 3 b) x = 2.
c) x = 3; x = -2. d) x = -3; x = 0; x = 2.
Đúng 1
Bình luận (0)
a) (x2 - 5x)2 + 10(x2 - 5x) + 24 = 0
b) (2x + 1)2 - 2x - 1 = 2
c) x(x - 1)(x2 - x + 1) - 6 = 0
d) (x2 + 1)2 + 3x(x2 + 1) + 2x2 = 0
a) Ta có: \(\left(x^2-5x\right)^2+10\left(x^2-5x\right)+24=0\)
\(\Leftrightarrow\left(x^2-5x\right)^2+4\left(x^2-5x\right)+6\left(x^2-5x\right)+24=0\)
\(\Leftrightarrow\left(x^2-5x\right)\left(x^2-5x+4\right)+6\left(x^2-5x+4\right)=0\)
\(\Leftrightarrow\left(x^2-5x+6\right)\left(x^2-5x+4\right)=0\)
\(\Leftrightarrow\left(x^2-2x-3x+6\right)\left(x^2-x-4x+4\right)=0\)
\(\Leftrightarrow\left[x\left(x-2\right)-3\left(x-2\right)\right]\left[x\left(x-1\right)-4\left(x-1\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-2=0\\x-3=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\\x=3\\x=4\end{matrix}\right.\)
Vậy: S={1;2;3;4}
b) Ta có: \(\left(2x+1\right)^2-2x-1=2\)
\(\Leftrightarrow\left(2x+1\right)^2-\left(2x+1\right)-2=0\)
\(\Leftrightarrow\left(2x+1\right)^2-2\left(2x+1\right)+\left(2x+1\right)-2=0\)
\(\Leftrightarrow\left(2x+1\right)\left(2x+1-2\right)+\left(2x+1-2\right)=0\)
\(\Leftrightarrow\left(2x+1+1\right)\left(2x-1\right)=0\)
\(\Leftrightarrow\left(2x+2\right)\left(2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+2=0\\2x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=-2\\2x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{1}{2}\end{matrix}\right.\)
Vậy: \(S=\left\{-1;\dfrac{1}{2}\right\}\)
c) Ta có: \(x\left(x-1\right)\left(x^2-x+1\right)-6=0\)
\(\Leftrightarrow x\left(x^3-x^2+x-x^2+x-1\right)-6=0\)
\(\Leftrightarrow x\left(x^3-2x^2+2x-1\right)-6=0\)
\(\Leftrightarrow x^4-2x^3+2x^2-x-6=0\)
\(\Leftrightarrow x^4-2x^3+2x^2-4x+3x-6=0\)
\(\Leftrightarrow x^3\left(x-2\right)+2x\left(x-2\right)+3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^3+2x+3\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^3-x+3x+3\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left[x\left(x^2-1\right)+3\left(x+1\right)\right]=0\)
\(\Leftrightarrow\left(x-2\right)\left[x\left(x-1\right)\left(x+1\right)+3\left(x+1\right)\right]=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)\left(x^2-x+3\right)=0\)
mà \(x^2-x+3>0\forall x\)
nên (x-2)(x+1)=0
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Vậy: S={2;-1}
d) Ta có: \(\left(x^2+1\right)^2+3x\left(x^2+1\right)+2x^2=0\)
\(\Leftrightarrow\left(x^2+1\right)^2+2x\left(x^2+1\right)+x\left(x^2+1\right)+2x^2=0\)
\(\Leftrightarrow\left(x^2+1\right)\left(x^2+1+2x\right)+x\left(x^2+1+2x\right)=0\)
\(\Leftrightarrow\left(x+1\right)^2\cdot\left(x^2+x+1\right)=0\)
mà \(x^2+x+1>0\forall x\)
nên x+1=0
hay x=-1
Vậy: S={-1}
Đúng 2
Bình luận (0)
Giải pt : a) 2/-x2+6x-8 - x-1/x-2 = x+3/x-4
b) 2/x3-x2-x+1 = 3/1-x2 - 1/x+1
c) x+2/x-2 - 2/x2-2x = 1/x
d) 5/-x2+5x-6 + x+3/2-x = 0
e) x/2x+2 - 2x/x2-2x-3 = x/6-2x
f) 1/x-1 - 3x2/x3-1 = 2x/x2+x-1
Bài 1: Giải các phương trình a/ c/ b/ d/ e/ (x +)(x-) 0 g/ (3x-1)(2x-3)(x+5) 0 h/ x2 – x 0 f/ x2 – 2x 0 i/ x2 – 3x 0 k/ (x+1)(x+2) (2-x)(x+2) Bài 4: Giải các phương trình sau:g) h) n) m) i/ 8 – x k) ...
Đọc tiếp
Bài 1: Giải các phương trình
|
|
a/ ![]() c/
c/ ![]()
b/ ![]() d/
d/ ![]()
e/ (x +![]() )(x-
)(x-![]() ) = 0 g/ (3x-1)(2x-3)(x+5) = 0
) = 0 g/ (3x-1)(2x-3)(x+5) = 0
h/ x2 – x = 0
f/ x2 – 2x = 0 i/ x2 – 3x = 0 k/ (x+1)(x+2) =(2-x)(x+2)
Bài 4: Giải các phương trình sau:
g) ![]() h)
h)![]()
n)  m)
m)
i/ ![]() = 8 – x k)
= 8 – x k) ![]() = – 4x +7
= – 4x +7
f. ![]()
Bài 6: Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
j/ 3x - (2x + 5 ) £ (2x – 3 ) k/ (x – 3)(x + 3) < x(x + 2 ) + 3
p/ 1+![]() q)
q) ![]()
b. ![]()
6:
k: =>x^2-9<x^2+2x+3
=>2x+3>-9
=>2x>-12
=>x>-6
1:
h: =>x(x-1)=0
=>x=0; x=1
i: =>x(x-3)=0
=>x=0; x=3
Đúng 0
Bình luận (0)
tìm x biết: a)x2 + 3x 0 b) x3 – 4x 0 c) 5x(x-1) x-1 d) 2(x+5) - x2-5x 0 e) 2x(x-5)-x(3+2x)26 f) 5x.(x – 2012) – x + 2012 0
Đọc tiếp
tìm x biết:
a)x2 + 3x = 0 b) x3 – 4x = 0
c) 5x(x-1) = x-1 d) 2(x+5) - x2-5x = 0
e) 2x(x-5)-x(3+2x)=26 f) 5x.(x – 2012) – x + 2012 = 0
a) \(\Rightarrow x\left(x+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=-3\end{matrix}\right.\)
b) \(\Rightarrow x\left(x^2-4\right)=0\Rightarrow x\left(x-2\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
c) \(\Rightarrow\left(x-1\right)\left(5x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{5}\end{matrix}\right.\)
d) \(\Rightarrow2\left(x+5\right)-x\left(x+5\right)=0\Rightarrow\left(x+5\right)\left(2-x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-5\\x=2\end{matrix}\right.\)
e) \(\Rightarrow2x^2-10x-3x-2x^2=26\)
\(\Rightarrow-13x=26\Rightarrow x=-2\)
f) \(\Rightarrow\left(x-2012\right)\left(5x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2012\\x=\dfrac{1}{5}\end{matrix}\right.\)
Đúng 1
Bình luận (0)