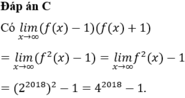Cho \(H=2^{2018}-2^{2017}-2^{2016}-...-2-1\). Tính \(2018^H\)

Những câu hỏi liên quan
B = 22018 - 22017 - 22016 - 22015 - 22014
\(B=2^{2018}-2^{2017}-2^{2016}-2^{2015}-2^{2014}\)
\(=>2B=2^{2019}-2^{2018}-2^{2017}-2^{2016}-2^{2015}\)
\(=>2B+B=2^{2019}-2^{2014}\)
\(=>B=\dfrac{2^{2019}-2^{2014}}{3}\)
Đúng 3
Bình luận (0)
Tìm dư của phép chia số A = 22021 + 22022 chia cho B = 1 + 2 + 22 + 23 +....+22016 + 22017
22018-22017
22018-22017
Giải:
Ta có: 22018 = 22017 . 2
=> 22018 - 22017 = 22017 . 2 - 22017 = 2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
B=1 + 1/2 + 1/3 + 1/4 +1/5 + .....+ 1/22016 - 2 + 1/22016 - 1 > 1008
Cho A=1+2+22+23+ ... +22018 , B=22019. Tính B - A
Ai làm đúng cho tick
\(A=1+2+2^2+...+2^{2018}\)
\(2A=2+2^3+2^4+...+2^{2019}\)
\(A=2A-A=1-2^{2019}\)
\(B-A=2^{2019}-\left(1-2^{2019}\right)\)
\(B-A=2^{2019}-1+2^{2019}\)
\(B-A=1\)
Đúng 2
Bình luận (1)
`#3107`
\(A=1+2+2^2+2^3+...+2^{2018}\) và \(B=2^{2019}\)
Ta có:
\(A=1+2+2^2+2^3+...+2^{2018}\)
\(2A=2+2^2+2^3+...+2^{2019}\)
\(2A-A=\left(2+2^2+2^3+...+2^{2019}\right)-\left(1+2+2^2+2^3+...+2^{2018}\right)\)
\(A=2+2^2+2^3+...+2^{2019}-1-2-2^2-2^3-...-2^{2018}\)
\(A=2^{2019}-1\)
Vậy, \(A=2^{2019}-1\)
Ta có:
\(B-A=2^{2019}-2^{2019}+1=1\)
Vậy, `B - A = 1.`
Đúng 1
Bình luận (0)
A = 1 + 2 + 22 + 23 + ... + 22018
2.A = 2 + 22 + 23 + 24 + ... + 22019
A = 22019 - 1
B - A = 22019 - (22019 - 1) = 1
Đúng 0
Bình luận (0)
Cho
l
i
m
x
→
∞
f
x
2
2018
.
Tính
l
i
m
x
→
∞
f
x
-
1
f...
Đọc tiếp
Cho l i m x → ∞ f x = 2 2018 . Tính l i m x → ∞ f x - 1 f x + 1 .
A. 2 2018 - 1
B. 4 2018 + 1
C. 4 2018 - 1
D. 2 2018 + 1
Cho hàm số
f
(
x
)
4
x
4
x
+
2
Tính tổng:
S
f
(
1
2017
)
+
f
(
2...
Đọc tiếp
Cho hàm số f ( x ) = 4 x 4 x + 2 Tính tổng:
S = f ( 1 2017 ) + f ( 2 2017 ) + . . . + f ( 2016 2017 )
A.S = 1007
B. S = 1009
C. S = 1008
D. S = 1006
Đáp án C
Chứng minh nhận xét: Nếu a + b = 1 thì ![]()
Đúng 0
Bình luận (0)
S = 2+2.22+3.23 +... +2016.22016
1) Chứng tỏ S+2013 chia hết cho 22017+1
2) Tìm số dư khi chia S cho 8
\(S=2+2.2^2+3.2^3+...+2016.2^{2016}\)
\(2S=2^2+2.2^3+3.2^4+...+2016.2^{2017}\)
\(2S-S=S=\text{}\text{}\text{}\text{}2^2+2.2^3+3.2^4+...+2016.2^{2017}-2-2.2^2-3.2^3-...-2016.2^{2016}\)
\(S=2\left(0-1\right)+2^2\left(1-2\right)+2^3\left(2-3\right)+...+2^{2016}\left(2015-2016\right)+2^{2017}.2016\)
\(S=-\left(2+2^2+2^3+...+2^{2016}\right)+2^{2017}.2016\)
\(\)Đặt \(A=2+2^2+2^3+...+2^{2016}\)
\(2A=2^2+2^3+2^4+...+2^{2017}\)
\(2A-A=A=2^2+2^3+2^4+...+2^{2017}-2-2^2-2^3-...-2^{2016}\)
\(A=2^{2017}-2\)
Thay vào S ta được:
\(S=-2^{2017}+2+2^{2017}.2016\)
\(S=2^{2017}.2015+2\)
Ta có \(S+2013=2^{2017}.2015+2+2013\)
\(S+2013=2^{2017}.2015+2015\)
\(S+2013=2015\left(2^{2017}+1\right)\)
Suy ra \(S+2013⋮2^{2017}+1\)
Vậy \(S+2013⋮2^{2017}+1\) (đpcm)
Đúng 3
Bình luận (0)
\(S=2+2.2^2+3.2^3+...+2016.2^{2016}\)
\(S=2+2^3+3.2^3+...+2016.2^{2016}\)
\(S=2+2^3\left(1+3+...+2016.2^{2013}\right)\)
\(S=2+8.\left(1+3+...+2016.2^{2013}\right)\)
Suy ra \(S\) chia \(8\) dư \(2\)
Vậy \(S\) chia \(8\) dư \(2\)
Gửi bạn nha, bài này làm hơi dài ^^
Đúng 0
Bình luận (0)
Cho số phức
z
-
1
+
3
i
2
. Tính giá trị của biểu thức
P
z
+
1
z
2016
+
z
2...
Đọc tiếp
Cho số phức z = - 1 + 3 i 2 . Tính giá trị của biểu thức
P = z + 1 z 2016 + z 2 + 1 z 2 2017 + z 3 + 1 z 3 2018 + z 4 + 1 z 4 2019 - 2 2018
A. P = 2019
B. P = -2019
C. P = 1
D. P = -1
Ta có
z = - 1 + 3 i 2 ⇒ 2 z + 1 = 3 i ⇒ 2 x + 1 2 = - 3
hay z 2 + z + 1 = 0 ⇔ z + 1 z = - 1
Khi đó:
z 2 = 1 z 2 = z + 1 z 2 - 2 = - 1 z 3 = 1 z 3 = z + 1 z 3 - 3 z + 1 z = 2 z 4 = 1 z 4 = z 2 + 1 z 2 - 2 = - 1
Như vậy
P = - 1 2016 + - 1 2017 + 2 2018 + - 1 2019 - 2 2018 = - 1
Đáp án D
Đúng 0
Bình luận (0)
Tính giá trị biểu thức (Thu gọn các tổng sau):
A = 2 + 22 + 23 + … + 22017
Ta có:
A = 2 + 22 + 23 + … + 22017
2A = 2.( 2 + 22 + 23 + … + 22017)
2A = 22 + 23 + 24 + … + 22018
2A – A = (22 + 23 + 24 + … + 22018) – (2 + 22 + 23 + … + 22017)
Vậy A = 22018 – 2
Đúng 3
Bình luận (0)