cho tam giác ABC , trung tuyến AM. từ M kẻ đường thẳng song song AB cắt AC tại N. biết AN=MN; BN cắt AM tại O.
Chứng minh : 1/ tam giác ABC cân tại A
2/ O là trọng tâm của tam giác ABC
Những câu hỏi liên quan
Bài 5: Cho tam giác ABC, trung tuyến AM. Từ M kẻ đường thẳng song song với AB cắt AC tại N. Biết AN=MN; BN cắt AM ở O. Chứng minh:
a) Tam giác ABC cân ở A
b) O là trọng tâm của tam giác ABC
a,Xét ΔΔAMN có : AN=NM
⇒⇒góc NAM =góc NMA
mà góc NMA= góc MAB (vì MN song song với AB)
nên góc NAM =góc MAB hay MA là tia phân giác góc BAC
Xét ΔΔABC ta có:
AM là tia phân giác góc BAC và cũng là đường trung tuyến ứng với cạnh BC
⇒⇒ΔΔABC cân tại A
b, Theo câu a ta có :ΔΔABC cân tại A
⇒⇒góc ABC = góc NCM
Mà góc NMC = góc ABC
NÊN góc NMC= góc NCM
⇒⇒ ΔΔNMC cân tại N
⇒⇒MN=NC
mà NM=AN
Nên AN=NC hay BN là đường trung tuyến ứng với cạnh AC
Ta có: AM là đường trung tuyến ứng với cạnh BC
BN là đường trung tuyến ứng với cạnh AC
mà BN cắt AM tại O
Nên O là trọng tâm của tam giác ABC
a,Xét ΔΔAMN có : AN=NM
⇒⇒góc NAM =góc NMA
mà góc NMA= góc MAB (vì MN song song với AB)
nên góc NAM =góc MAB hay MA là tia phân giác góc BAC
Xét ΔΔABC ta có:
AM là tia phân giác góc BAC và cũng là đường trung tuyến ứng với cạnh BC
⇒⇒ΔΔABC cân tại A
b, Theo câu a ta có :ΔΔABC cân tại A
⇒⇒góc ABC = góc NCM
Mà góc NMC = góc ABC
NÊN góc NMC= góc NCM
⇒⇒ ΔΔNMC cân tại N
⇒⇒MN=NC
mà NM=AN
Nên AN=NC hay BN là đường trung tuyến ứng với cạnh AC
Ta có: AM là đường trung tuyến ứng với cạnh BC
BN là đường trung tuyến ứng với cạnh AC
mà BN cắt AM tại O
Nên O là trọng tâm của tam giác ABC
Đúng 2
Bình luận (0)
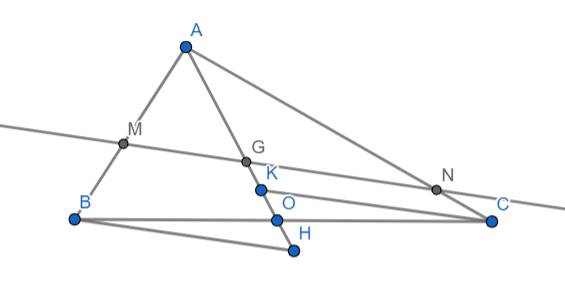
Cho tam giác ABC có trung tuyến AO, trọng tâm G, đường thănhr đi qua G cắt AB và AC lần lượt tại M và N. Từ BC kẻ đg thẳng song song với MN cắt AO lần lượt tại H và K Cm AB/AM+AC/AN=3
Xét 2 tam giác AMG và ABH ta có:
\(\widehat{BAH}\) chung
\(\widehat{AMG}=\widehat{ABH}\) (cặp góc đồng vị do BH//MG)
\(\Rightarrow\Delta AMG\sim\Delta ABH\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{AH}{AG}\) (1)
Xét 2 tam giác ANG và ACK có:
\(\widehat{CAK}\) chung
\(\widehat{ANG}=\widehat{ACK}\) (cặp góc đồng vị do CK//GN)
\(\Rightarrow\Delta ANG\sim\Delta ACK\left(g.g\right)\)
\(\Rightarrow\dfrac{AC}{AN}=\dfrac{AK}{AG}\) (2)
Xét hai tam giác BOH và COK ta có:
\(\widehat{BOH}=\widehat{COK}\) (đối đỉnh)
\(BO=CO\) (AO là đường trung tuyến nên O là trung điểm của BC)
\(\widehat{HBO}=\widehat{KCO}\) (so le trong vì BH//MN và CK//MN ⇒ BH//CK)
\(\Rightarrow\Delta BOH=\Delta COK\left(g.c.g\right)\)
\(\Rightarrow HO=OK\) (hai cạnh t.ứng)
\(\Rightarrow HK=2HO\)
Ta lấy (1) + (2) \(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{AH+AK}{AG}=\dfrac{AH+AH+HK}{AG}=\dfrac{2AH+HK}{AG}\)
\(=\dfrac{2AH+2HO}{AG}=\dfrac{2\left(AH+HO\right)}{AG}=\dfrac{2AO}{AG}\)
Mà G là trọng tâm của tam giác ABC \(\Rightarrow AO=\dfrac{3}{2}AG\)
\(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{2\cdot\dfrac{3}{2}AG}{AG}=2\cdot\dfrac{3}{2}=3\left(đpcm\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC trung tuyến AM. Từ M kẻ đường thẳng song song với AB cắt AC ở N. Biết AN=MN, BN cắt AM ở O. Chứng minh:
a) tam giác ABC cân ở A
b) O là trọng tâm của tam giác ABC
cho tam giác ABC ,trung tuyến AM .từ M kẻ đường thẳng song song với AB cắt AC tại N . biết AN=MN,BN cắt AM ở O .
CMR:A)tam giác ABC CÂN TẠI A.
B) O LÀ TRỌNG TÂM CỦA TAM GIÁC ABC
<br class="Apple-interchange-newline"><div id="inner-editor"></div>ΔABC, có: M là trung điểm BC và MN //BC
=> MN là đường trung bình ΔABC
=> N là trung điểm NC
=> AN=NC mà AN=MN (gt) => MN=NC
Xét ΔMNC, có : MN=NC
=> ΔMNC cân tại N
=> góc M= góc C (1)
Vì MN//AB
=> góc B= góc M( 2 góc đồng vị) (2)
Từ (1) và (2) => góc B= góc C
Xét ΔABC, có : góc B= góc C
=>
<br class="Apple-interchange-newline"><div id="inner-editor"></div>ΔABC, có: M là trung điểm BC và MN //BC
=> MN là đường trung bình ΔABC
=> N là trung điểm NC
=> AN=NC mà AN=MN (gt) => MN=NC
Xét ΔMNC, có : MN=NC
=> ΔMNC cân tại N
=> góc M= góc C (1)
Vì MN//AB
=> góc B= góc M( 2 góc đồng vị) (2)
Từ (1) và (2) => góc B= góc C
Xét ΔABC, có : góc B= góc C
=> ΔABC cân tại A
Đúng 0
Bình luận (0)
Cho tam giác ABC, M lá trung điểm của AB, kẻ đường thẳng qua M song song với BC cắt AC tại N. Từ N kẻ đường thẳng song song với AB cắt BC tại P. Chứng minh rằng
a)tam giác BMN = tam giác NPB và AM = NP
b)tam giác AMN = tam giác NPC và AN = NC
huhu mình mong các bạn có thể làm nhanh lên cho mình
Đúng 0
Bình luận (0)
Câu a)
Xét tam giác ANM và tam giác CNE có :
MN = NE ( GT )
AN = NC ( GT )
góc ANM = góc CNE ( 2 góc đối đỉnh )
=> tam giác ANM = tam giác CNE ( cgc )
=> CE = AM ( cặp cạnh tương ứng )
Mà AM = BM ( do M là trung điểm AB )
=> BM = CE
Vậy BM = CE
Câu b)
Do tam giác ANM = tam giác CNE ( CMT )
=> góc MAN = góc NCE ( cặp góc tương ứng )
Mà 2 góc ở vị trí so le trong
=> AM // CE
=> góc BMC = góc MCE ( 2 góc ở vị trí so le trong )
Xét tam giác BMC và tam giác ECM có :
BM = EC ( CMT )
MC : chung
góc BMC = góc MCE ( CMT )
=> tam giác BMC = tam giác ECM ( cgc )
=> ME = BC ( cặp cạnh tương ứng )
Mà MN = ME/2 ( GT )
=> MN = BC/2
Do tam giác BMC = tam giác ECM ( CMT )
=> góc MCB = góc CME ( cặp góc tương ứng )
Mà 2 góc ở vị trí so le trong
=> ME //BC
Hay MN//BC
Vậy.....
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tam giác ABC. kẻ trung tuyến am. từ một điểm D thuộc AM kẻ đường thẳng song song AB cắt AC và BC tại E và F, dường thẳng song song với AC kẻ từ F cắt AB tại H. kẻ từ M đường thẳng song song AC, AB cắt AB tại Q, cắt AC tại F. chứng minh BH/BQ=DE/MK
Cho tam giác ABC đường trung tuyến AM từ M kẻ đường thẳng song song với AB cắt AC tại M biết AM = NM . BN cắt AM ở đỉnh O . C/M
a) tam giác ABC là tam giác cân và AM là đường trung trực của đoạn thẳng BC
b) N là trung điểm của AC
c) gọi k là trung điểm của AB . C/M 3 điểm C, O, K thẳng hàng
Cho tam giác ABC đường trung tuyến AM từ N kẻ đường thẳng song song với AB cắt AC tại M biết AN MN . BN cắt AM ở đỉnh O . Chứng minh a) tam giác ABC cân ở A và AM là đường trung trực của đoạn thẳng BC b) N lac là trung điểm của AC c) gọi K là trung điểm của AB . Chứng minh 3 điểm C, O , K thẳng hàngBạn nào trả lời đc câu b và câu c mình sẽ kết bạn với bạn ấy và like
Đọc tiếp
Cho tam giác ABC đường trung tuyến AM từ N kẻ đường thẳng song song với AB cắt AC tại M biết AN = MN . BN cắt AM ở đỉnh O . Chứng minh
a) tam giác ABC cân ở A và AM là đường trung trực của đoạn thẳng BC
b) N lac là trung điểm của AC
c) gọi K là trung điểm của AB . Chứng minh 3 điểm C, O , K thẳng hàng
Bạn nào trả lời đc câu b và câu c mình sẽ kết bạn với bạn ấy và like
Cho tam giác ABC có AB=12cm , AC=15cm, BC=q6cm. Trên cạnh AB lấy điểm M sao cho AM=3cm. Từ M kẻ đường thẳng song song với BC cắt AC tại N, cắt trung tuyến AI tại K.
a/ Tính độ dài MN
b/ Chứng minh K là trung điểm của MN
c/ Trên tia MN lấy điểm P sao cho MP=8cm. Nối PI cắt AC tại Q. Chững minh tam giác QIC đồng dạng với tam giác AMN
Bài 3. Cho tam giác
ABC
. Trên cạnh
AC
lấy điểm
N
sao cho
2
5
CN
AN
. Trên cạnh BC lấy điểm
M
sao cho
BC xMC
và MN // AB.
Tìm x.
A. 5 B. 2,5 C. 3,5 D. 1,4
Đúng 0
Bình luận (0)