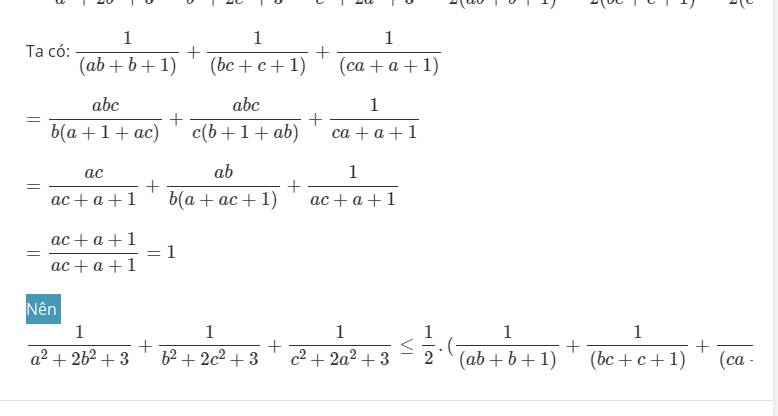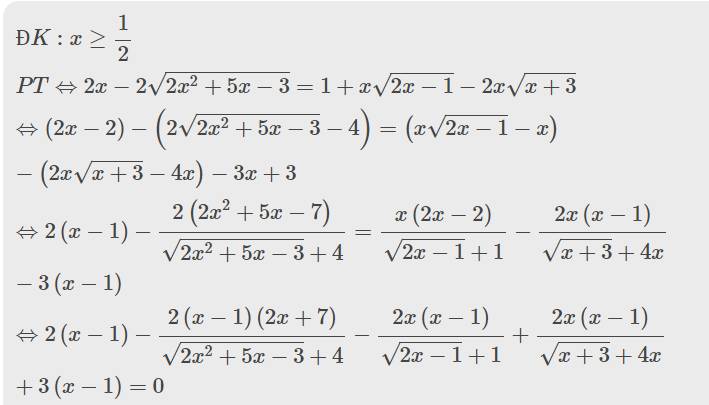Đặt \(a=\frac{1}{x};b=\frac{2}{y};c=\frac{3}{z}\)

Theo bài ra, ta có:

 x+y+z=3

\(bđt\Leftrightarrow\frac{x^3}{x^2+y^2}+\frac{y^3}{y^2+z^2}+\frac{z^3}{z^2+x^2}\ge\frac{3}{2}\)

Áp dụng kĩ thuật Cau-chy ngược dấu ta có:

\(\frac{x^3}{x^2+y^2}+\frac{y^3}{y^2+z^2}+\frac{z^3}{z^2+x^2}\ge\frac{x+y+z}{2}=\frac{3}{2}\)

Dấu '=' xảy ra <=> a=3;b=2;c=1

*Bài khá giống bạn kia :)

Đặt \(a=\frac{1}{x};b=\frac{2}{y};c=\frac{3}{z}\)

\(\Rightarrow x+y+z=3\)

BĐT cần chứng minh trở thành :

\(\frac{x^3}{x^2+y^2}+\frac{y^3}{y^2+z^2}+\frac{z^3}{z^2+x^2}\ge\frac{3}{2}\)

Áp dụng kĩ thuật Cô Si ngược dấu ta có :

\(\frac{x^3}{x^2+y^2}+\frac{y^3}{y^2+z^2}+\frac{z^3}{z^2+x^2}\ge\frac{x+y+z}{2}=\frac{3}{2}\)

Dấu đẳng thức xảy ra \(\Leftrightarrow a=3;b=2;c=1\) 

\(\dfrac{1}{\left(a+b+a+c\right)^2}\le\dfrac{1}{4\left(a+b\right)\left(a+c\right)}=\dfrac{1}{4\left(a^2+ab+bc+ca\right)}\le\dfrac{1}{64}\left(\dfrac{1}{a^2}+\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\right)\)

\(\le\dfrac{1}{64}\left(\dfrac{1}{a^2}+\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)=\dfrac{1}{64}\left(\dfrac{2}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)\)

Tương tự và cộng lại:

\(P\le\dfrac{1}{64}\left(\dfrac{4}{a^2}+\dfrac{4}{b^2}+\dfrac{4}{c^2}\right)=\dfrac{1}{16}.3=\dfrac{3}{16}\)

Dấu "=" xảy ra khi \(a=b=c=1\)

Áp dụng bđt: \(\dfrac{1}{x+y}\le\dfrac{1}{4}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\left(1\right)\)

\(\dfrac{1}{2a+b+c}=\dfrac{1}{\left(a+b\right)+\left(a+c\right)}\le\dfrac{1}{4}\left(\dfrac{1}{a+b}+\dfrac{1}{a+c}\right)\)

\(\Rightarrow P\le\dfrac{1}{16}\left[\left(\dfrac{1}{a+b}+\dfrac{1}{a+c}\right)^2+\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}\right)^2+\left(\dfrac{1}{b+c}+\dfrac{1}{a+c}\right)^2\right]\)\(\Rightarrow16P\le\dfrac{2}{\left(a+b\right)^2}+\dfrac{2}{\left(b+c\right)^2}+\dfrac{2}{\left(a+c\right)^2}+\dfrac{2}{\left(a+b\right)\left(b+c\right)}+\dfrac{2}{\left(a+b\right)\left(b+c\right)}+\dfrac{2}{\left(b+c\right)\left(c+a\right)}\)

Áp dụng: \(x^2+y^2+z^2\ge xy+yz+xz\left(2\right)\) với a+b=x,b+c=y,c+a=z

\(\Rightarrow16P\le\dfrac{4}{\left(a+b\right)^2}+\dfrac{4}{\left(b+c\right)^2}+\dfrac{4}{\left(c+a\right)^2}\)

Ta có: \(\dfrac{1}{\left(a+b\right)^2}\le4.16.\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2\)(do (1))

\(\Rightarrow16P\le\dfrac{1}{4}.16\left[\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2+\left(\dfrac{1}{b}+\dfrac{1}{c}\right)^2+\left(\dfrac{1}{c}+\dfrac{1}{a}\right)^2\right]=\dfrac{1}{4}\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}+\dfrac{2}{ab}+\dfrac{2}{bc}+\dfrac{2}{ca}\right)\le\dfrac{1}{4}.4.\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)=3\)(do(2) và \(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}=3\))

\(\Rightarrow P\le\dfrac{3}{16}\)

\(ĐTXR\Leftrightarrow a=b=c=1\)

Đặt \(P=\dfrac{1}{a^3\left(b+c\right)}+\dfrac{1}{b^3\left(c+a\right)}+\dfrac{1}{c^3\left(a+b\right)}\)

\(P=\dfrac{\left(abc\right)^2}{a^3\left(b+c\right)}+\dfrac{\left(abc\right)^2}{b^3\left(c+a\right)}+\dfrac{\left(abc\right)^2}{c^3\left(a+b\right)}\)

\(P=\dfrac{\left(bc\right)^2}{a\left(b+c\right)}+\dfrac{\left(ca\right)^2}{b\left(c+a\right)}+\dfrac{\left(ab\right)^2}{c\left(a+b\right)}\)

\(P\ge\dfrac{\left(bc+ca+ab\right)^2}{a\left(b+c\right)+b\left(c+a\right)+c\left(a+b\right)}\) (BĐT B.C.S)

\(=\dfrac{ab+bc+ca}{2}\) \(\ge\dfrac{3\sqrt[3]{abbcca}}{2}=\dfrac{3}{2}\) (do \(abc=1\)).

ĐTXR \(\Leftrightarrow a=b=c=1\)

Đề bài sai với \(a=b=c=2\)

đề đúng nhớ áp dụng AM-GM

AD bđt AM-GM cho 3 số

\(\dfrac{b^2c}{a^3\left(b+c\right)}+\dfrac{b+C}{4bc}+\dfrac{1}{2b}\ge3\sqrt[3]{\dfrac{b^2c}{a^3\left(b+c\right)}.\dfrac{\left(b+c\right)}{4bc}.\dfrac{1}{2b}}=\dfrac{3}{2a}\)

\(\Rightarrow\dfrac{b^2c}{a^3\left(b+c\right)}\ge\dfrac{3}{2a}-\dfrac{3}{4b}-\dfrac{1}{4c}\)

thiết lập bđt tương tự r cộng lại \(\Rightarrow\dfrac{b^2c}{a^3\left(b+c\right)}+\dfrac{c^2a}{b^3\left(c+a\right)}+\dfrac{a^2b}{c^3\left(a+b\right)}\ge\left(\dfrac{3}{2}-\dfrac{3}{4}-\dfrac{1}{4}\right)\left(a+b+c\right)=\dfrac{1}{2}\left(a+b+c\right)\)