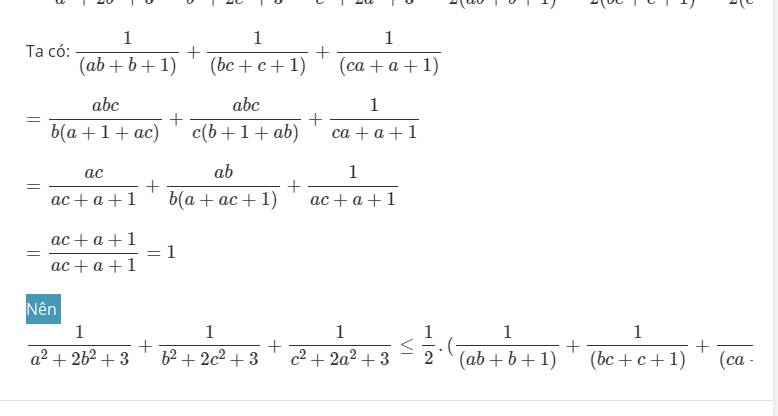Ôn tập chương 1: Căn bậc hai. Căn bậc ba
Các câu hỏi tương tự
từ giả thiết, ta có dfrac{1}{xy}+dfrac{1}{yz}+dfrac{1}{zx}1
đặt left(dfrac{1}{xy};dfrac{1}{yz};dfrac{1}{zx}right)left(a;b;cright)Rightarrow a+b+c1 left(dfrac{ac}{b};dfrac{ab}{c};dfrac{bc}{a}right)left(dfrac{1}{x^2};dfrac{1}{y^2};dfrac{1}{z^2}right)
ta có VTdfrac{1}{sqrt{1+dfrac{1}{x^2}}}+dfrac{1}{sqrt{1+dfrac{1}{y^2}}}+dfrac{1}{sqrt{1+dfrac{1}{z^1}}}sqrt{dfrac{1}{1+dfrac{ac}{b}}}+sqrt{dfrac{1}{1+dfrac{ab}{c}}}+sqrt{dfrac{1}{1+dfrac{bc}{a}}}
dfrac{1}{sqrt{dfrac{b+ac}{b}}}+dfrac{1}{sqrt{dfrac...
Đọc tiếp
từ giả thiết, ta có \(\dfrac{1}{xy}+\dfrac{1}{yz}+\dfrac{1}{zx}=1\)
đặt \(\left(\dfrac{1}{xy};\dfrac{1}{yz};\dfrac{1}{zx}\right)=\left(a;b;c\right)\Rightarrow a+b+c=1\) =>\(\left(\dfrac{ac}{b};\dfrac{ab}{c};\dfrac{bc}{a}\right)=\left(\dfrac{1}{x^2};\dfrac{1}{y^2};\dfrac{1}{z^2}\right)\)
ta có VT=\(\dfrac{1}{\sqrt{1+\dfrac{1}{x^2}}}+\dfrac{1}{\sqrt{1+\dfrac{1}{y^2}}}+\dfrac{1}{\sqrt{1+\dfrac{1}{z^1}}}=\sqrt{\dfrac{1}{1+\dfrac{ac}{b}}}+\sqrt{\dfrac{1}{1+\dfrac{ab}{c}}}+\sqrt{\dfrac{1}{1+\dfrac{bc}{a}}}\)
=\(\dfrac{1}{\sqrt{\dfrac{b+ac}{b}}}+\dfrac{1}{\sqrt{\dfrac{a+bc}{a}}}+\dfrac{1}{\sqrt{\dfrac{c+ab}{c}}}=\sqrt{\dfrac{a}{\left(a+b\right)\left(a+c\right)}}+\sqrt{\dfrac{b}{\left(b+c\right)\left(b+a\right)}}+\sqrt{\dfrac{c}{\left(c+a\right)\left(c+b\right)}}\)
\(\le\sqrt{3}\sqrt{\dfrac{ac+ab+bc+ba+ca+cb}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}}=\sqrt{3}.\sqrt{\dfrac{2\left(ab+bc+ca\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}}\)
ta cần chứng minh \(\sqrt{\dfrac{2\left(ab+bc+ca\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}}\le\dfrac{3}{2}\Leftrightarrow\dfrac{2\left(ab+bc+ca\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\le\dfrac{9}{4}\Leftrightarrow8\left(ab+bc+ca\right)\le9\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
<=>\(8\left(a+b+c\right)\left(ab+bc+ca\right)\le9\left(a+b\right)\left(b+c\right)\left(c+a\right)\) (luôn đúng )
^_^
bài 1. Cho a = 2; b = 8; c = \(\sqrt{5}\) - 2
a) Tính M \(\sqrt{a}.\sqrt{b}\)
b) Tính N \(\sqrt{c^2}-\dfrac{1}{c}\)
c) Tìm x biết rằng \(2x^2+c\left(2c-\sqrt{a}\right)-c\sqrt{2}=0\)
Giải PT:a) dfrac{1}{2}sqrt{x-1}-dfrac{3}{2}sqrt{9x-9}+24sqrt{dfrac{x-1}{64}}-17b) sqrt{18x-9}-0,5sqrt{2x-1}+dfrac{1}{2}sqrt{25left(2x-1right)}+sqrt{49left(2x-1right)}24c) sqrt{36x-72}-15sqrt{dfrac{x-2}{25}}4left(5+sqrt{x-2}right)d) sqrt{dfrac{1}{3x+2}}-dfrac{1}{2}sqrt{dfrac{9}{3x+2}}+sqrt{dfrac{16}{3x+2}}-5sqrt{dfrac{1}{12x+8}}1e) dfrac{1}{2}sqrt{dfrac{49x}{x+2}}-3sqrt{dfrac{x}{4x+8}}-sqrt{dfrac{x}{x+2}}-sqrt{5}0
Đọc tiếp
Giải PT:
a) \(\dfrac{1}{2}\sqrt{x-1}-\dfrac{3}{2}\sqrt{9x-9}+24\sqrt{\dfrac{x-1}{64}}=-17\)
b) \(\sqrt{18x-9}-0,5\sqrt{2x-1}+\dfrac{1}{2}\sqrt{25\left(2x-1\right)}+\sqrt{49\left(2x-1\right)}=24\)
c) \(\sqrt{36x-72}-15\sqrt{\dfrac{x-2}{25}}=4\left(5+\sqrt{x-2}\right)\)
d) \(\sqrt{\dfrac{1}{3x+2}}-\dfrac{1}{2}\sqrt{\dfrac{9}{3x+2}}+\sqrt{\dfrac{16}{3x+2}}-5\sqrt{\dfrac{1}{12x+8}}=1\)
e) \(\dfrac{1}{2}\sqrt{\dfrac{49x}{x+2}}-3\sqrt{\dfrac{x}{4x+8}}-\sqrt{\dfrac{x}{x+2}}-\sqrt{5}=0\)
DẠNG TOÁN RÚT GỌN:
1) a) Chứng tỏ: dfrac{5+3sqrt{5}}{sqrt{5}}+dfrac{3+sqrt{3}}{sqrt{3}+1}-left(sqrt{5}+3right)sqrt{3}
b) Cho P a-left(dfrac{1}{sqrt{a}-sqrt{a-1}}-dfrac{1}{sqrt{a}+sqrt{a+1}}right)left(a1right). Chứng tỏ P 0
2) Giải phương trình: a) 3x +sqrt{2} 2(x+sqrt{2})
b) 3sqrt{x-2}-sqrt{x^2-4}0
3) Thực hiện phép tính:
a) sqrt[.3]{2-10}-sqrt{36+64}
b) sqrt{left(sqrt{2}-3right)^2}+sqrt[3]{left(sqrt{2}-5right)^3}
4) Cho biểu thức: P dfrac{2a^2+4}{1-a^3}-dfrac{1}{1+sqrt{a}}-dfrac{1}{1-...
Đọc tiếp
DẠNG TOÁN RÚT GỌN:
1) a) Chứng tỏ: \(\dfrac{5+3\sqrt{5}}{\sqrt{5}}+\dfrac{3+\sqrt{3}}{\sqrt{3}+1}-\left(\sqrt{5}+3\right)=\sqrt{3}\)
b) Cho P= \(a-\left(\dfrac{1}{\sqrt{a}-\sqrt{a-1}}-\dfrac{1}{\sqrt{a}+\sqrt{a+1}}\right)\left(a>=1\right)\). Chứng tỏ P >= 0
2) Giải phương trình: a) 3x +\(\sqrt{2}\) = 2(x+\(\sqrt{2}\))
b) \(3\sqrt{x-2}-\sqrt{x^2-4}=0\)
3) Thực hiện phép tính:
a) \(\sqrt[.3]{2-10}-\sqrt{36+64}\)
b) \(\sqrt{\left(\sqrt{2}-3\right)^2}+\sqrt[3]{\left(\sqrt{2}-5\right)^3}\)
4) Cho biểu thức: P= \(\dfrac{2a^2+4}{1-a^3}-\dfrac{1}{1+\sqrt{a}}-\dfrac{1}{1-\sqrt{a}}\)
a) Tìm điều kiện của a để P xác định
b) Rút gọn biểu thức P
Cho a;b;c >0 thỏa mãn \(a+b+c=\dfrac{1}{abc}\)
Cmr: \(\sqrt{\dfrac{\left(1+b^2c^2\right)\left(1+a^2c^2\right)}{c^2+a^2b^2c^2}}=a+b\)
Giúp em với ạ. Em cảm ơn các anh/chị ạ.
Bài 1: Thực hiện phép tính
a) dfrac{1}{2}sqrt{48}-sqrt{32}-sqrt{75}-dfrac{1}{5}sqrt{50}
b) dfrac{3+sqrt{3}}{3-sqrt{3}}+dfrac{3-sqrt{3}}{3+sqrt{3}}
c) 4sqrt{dfrac{3}{2}}-dfrac{5}{2}sqrt{24}+dfrac{1}{2}sqrt{50}
d) left(2sqrt{5}+5sqrt{2}right).sqrt{5}-sqrt{250}
Bài 2: Rút gọn biểu thức sau
sqrt{9a}-sqrt{16a}+sqrt{49a} với age0
Bài 3: Cho biểu thức sau
Aleft(dfrac{sqrt{x}}{sqrt{x}-a}+dfrac{sqrt{x}}{sqrt{x}+2}right).dfrac{4-x}{2sqrt{x}}với x0và xne4
a) Rút gọn A b) Tìm x để...
Đọc tiếp
Bài 1: Thực hiện phép tính
a) \(\dfrac{1}{2}\sqrt{48}-\sqrt{32}-\sqrt{75}\)\(-\dfrac{1}{5}\sqrt{50}\)
b) \(\dfrac{3+\sqrt{3}}{3-\sqrt{3}}+\dfrac{3-\sqrt{3}}{3+\sqrt{3}}\)
c) \(4\sqrt{\dfrac{3}{2}}-\dfrac{5}{2}\sqrt{24}+\dfrac{1}{2}\sqrt{50}\)
d) \(\left(2\sqrt{5}+5\sqrt{2}\right).\sqrt{5}-\sqrt{250}\)
Bài 2: Rút gọn biểu thức sau
\(\sqrt{9a}-\sqrt{16a}+\sqrt{49a}\) với \(a\ge0\)
Bài 3: Cho biểu thức sau
A=\(\left(\dfrac{\sqrt{x}}{\sqrt{x}-a}+\dfrac{\sqrt{x}}{\sqrt{x}+2}\right).\dfrac{4-x}{2\sqrt{x}}\)với \(x>0\)và \(x\ne4\)
a) Rút gọn A b) Tìm x để A=-3
Bài 4: Rút gọn biểu thức sau
A=\(\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{1}{1+\sqrt{x}}\right):\dfrac{1}{x-1}\) với \(x\ge0\) và \(x\ne1\)
Bài 5: Cho biểu thức
C= \(\left(\dfrac{2+\sqrt{a}}{2-\sqrt{a}}-\dfrac{2-\sqrt{a}}{2+\sqrt{a}}-\dfrac{4a}{a-4}\right):\left(\dfrac{2}{2-\sqrt{a}}-\dfrac{\sqrt{a}+3}{2\sqrt{a}-a}\right)\)
a) Rút gọn C b) Timg giá trị của a để C>0 c) Tìm giá trị của a để C=-1
Bài 6: Giải phương trình
a) \(2\sqrt{3}-\sqrt{4+x^2}=0\\\)
b) \(\sqrt{16x+16}-\sqrt{9x+9}=1\)
c) \(3\sqrt{2x}+5\sqrt{8x}-20-\sqrt{18x}=0\)
d) \(\sqrt{4\left(x+2\right)^2}=8\)
Câu 1:
Cho biểu thức: f_{left(xright)} dfrac{2left(1-sqrt{x}right)}{sqrt{x}+1}+dfrac{sqrt{x}+4}{sqrt{x}-4}+dfrac{xleft(sqrt{x}-3right)-2left(5sqrt{x}+8right)}{x-3sqrt{x}-4}
a) Rút gọn biểu thức f_{left(xright)}
b) Tìm x để f_{left(xright)} đạt GTNN
Câu 2:
Giải PT: 2left(x-1right)^23left(sqrt{x^3+2x^2-2x+3}+2right)
Câu 3:
Tìm nghiệm nguyên của PT: 9x+5y+182xy
Câu 4:
a) Giải PT: 2x^2+2x+1sqrt{4x+1}
b) Giải hệ phương trình: left{{}begin{matrix}left|x-2right|+2left|y-1right|9x+left|y-1r...
Đọc tiếp
Câu 1:
Cho biểu thức: \(f_{\left(x\right)}=\) \(\dfrac{2\left(1-\sqrt{x}\right)}{\sqrt{x}+1}+\dfrac{\sqrt{x}+4}{\sqrt{x}-4}+\dfrac{x\left(\sqrt{x}-3\right)-2\left(5\sqrt{x}+8\right)}{x-3\sqrt{x}-4}\)
a) Rút gọn biểu thức \(f_{\left(x\right)}\)
b) Tìm x để \(f_{\left(x\right)}\) đạt GTNN
Câu 2:
Giải PT: \(2\left(x-1\right)^2=3\left(\sqrt{x^3+2x^2-2x+3}+2\right)\)
Câu 3:
Tìm nghiệm nguyên của PT: \(9x+5y+18=2xy\)
Câu 4:
a) Giải PT: \(2x^2+2x+1=\sqrt{4x+1}\)
b) Giải hệ phương trình: \(\left\{{}\begin{matrix}\left|x-2\right|+2\left|y-1\right|=9\\x+\left|y-1\right|=-1\end{matrix}\right.\)
Câu 5:
a) Cho S = \(1+3+3^2+3^3+3^4+...+3^{98}+3^{99}\)
Chứng minh: S \(⋮\) 40
b) Rút gọn phân thức: \(\dfrac{a^3+b^3+c^3-3abc}{\left(a-b\right)^2+\left(a-c\right)^2+\left(b-c\right)^2}\)
P=\(\left(\dfrac{2\left(a+b\right)}{\sqrt{a^3}-2\sqrt{2b^3}}-\dfrac{\sqrt{a}}{a+\sqrt{2ab}+2b}\right)\left(\dfrac{\sqrt{a^3}+2\sqrt{2b^3}}{2b+\sqrt{2ab}}-\sqrt{a}\right)\)
a) Tìm điều kiện của a và b để biểu thức P xác định. Rút gọn P
b) Biết \(a=1+\dfrac{\sqrt{3}}{2}\) và \(b=\dfrac{1}{2}-\dfrac{\sqrt{3}}{4}\). Tính giá trị biểu thức P
Chứng minh đẳng thức:
a) dfrac{xsqrt{x}+ysqrt{y}}{sqrt{x}+sqrt{y}}-left(sqrt{x}-sqrt{y}right)^2sqrt{xy}left(xge0,yge0,x^2+y^2ne0right)
b) left(dfrac{1}{a-sqrt{a}}+dfrac{1}{sqrt{a}-1}right):dfrac{sqrt{a}+1}{a-2sqrt{a}+1}left(age0,ane1right)
c) sqrt{x+2sqrt{x-2}-1}left(sqrt{x-2}-1right):left(sqrt{x}-sqrt{3}right)sqrt{x}+sqrt{3}left(xge2,xne3right)
Đọc tiếp
Chứng minh đẳng thức:
a) \(\dfrac{x\sqrt{x}+y\sqrt{y}}{\sqrt{x}+\sqrt{y}}-\left(\sqrt{x}-\sqrt{y}\right)^2=\sqrt{xy}\left(x\ge0,y\ge0,x^2+y^2\ne0\right)\)
b) \(\left(\dfrac{1}{a-\sqrt{a}}+\dfrac{1}{\sqrt{a}-1}\right):\dfrac{\sqrt{a}+1}{a-2\sqrt{a}+1}\left(a\ge0,a\ne1\right)\)
c) \(\sqrt{x+2\sqrt{x-2}-1}\left(\sqrt{x-2}-1\right):\left(\sqrt{x}-\sqrt{3}\right)=\sqrt{x}+\sqrt{3}\left(x\ge2,x\ne3\right)\)