Tìm m để đa thức \(P\left(x\right)=x^4+x^3+6x^2-40x+m-2017\)chia hết cho x+2

Những câu hỏi liên quan
Tìm các số a, b để đa thức \(f\left(x\right)=6x^4-7x^3+ax^2+3x+2\) chia hết cho đa thức \(f_2\left(x\right)=x^2-x+b\)
Cho đa thức P(x)= x^4+x^3+6x^2-40x+m=1979.
a, Tìm m sao cho P(x) chia hết cho x-2
b, Với m vừa tìm được, giải phương trình P(x)=0
Cho đa thức \(f\left(x\right)=6x^3-7x^2-16x+m\cdot f\left(x\right)\) chia hết cho \(2x-5\). Tìm \(m\) và số dư phép chia \(f\left(x\right)\) cho \(3x-2\).
\(f\left(x\right)=6x^3-7x^2-16x+m\)
Do \(f\left(x\right)\) chia hết \(2x-5\), theo định lý Bezout:
\(f\left(\dfrac{5}{2}\right)=0\Rightarrow6.\left(\dfrac{5}{2}\right)^3-7.\left(\dfrac{5}{2}\right)^2-16.\left(\dfrac{5}{2}\right)+m=0\)
\(\Rightarrow m=-10\)
Khi đó \(f\left(x\right)=6x^3-7x^2-16x-10\)
Số dư phép chia cho \(3x-2\):
\(f\left(\dfrac{2}{3}\right)=6.\left(\dfrac{2}{3}\right)^3-7.\left(\dfrac{2}{3}\right)^2-16.\left(\dfrac{2}{3}\right)-10=-22\)
Đúng 5
Bình luận (0)
Do chia hết , theo định lý Bezout:
Khi đó
Số dư phép chia cho :
Đúng 0
Bình luận (0)
\(f\left(x\right)=6x^3-7x^2-16x+m\)
Do \(f\left(x\right)⋮2x-5\) , theo định lý Bezout:
\(f\left(\dfrac{5}{2}\right)=0\Rightarrow6\left(\dfrac{5}{2}\right)^3-7\left(\dfrac{5}{2}\right)^2-16\left(\dfrac{5}{2}\right)+m=0\)
\(\Rightarrow m=-10\)
Khi đó \(f\left(x\right)=6x^3-7x^2-16x-10\)
Số dư phép chia cho \(3x-2:\)
\(f\left(\dfrac{2}{3}\right)=6\left(\dfrac{2}{3}\right)^3-7\left(\dfrac{2}{3}\right)^2-16\left(\dfrac{2}{3}\right)-10=-22\)
Đúng 0
Bình luận (0)
tìm a,b để đa thứ f(x) chia hết cho đa thức g(x)
\(a.f\left(x\right)=x^4-9x^3+21x^2+ax+b: g\left(x\right)=x^2-x-1\)
\(b.f\left(x\right)=x^4-x^3+6x^2-x+a: g\left(x\right)=x^2-x+5\)
\(c.f\left(x\right)=3x^3+10x^2-5+a: g\left(x\right)=3x+1\)
em chưa cho đa thức f(x) và g(x) nà
Đúng 0
Bình luận (1)
a: \(\dfrac{f\left(x\right)}{g\left(x\right)}\)
\(=\dfrac{x^4-9x^3+21x^2+ax+b}{x^2-x-1}\)
\(=\dfrac{x^4-x^3-x^2-8x^3+8x^2+8x+14x^2-14x-14+\left(a+6\right)x+b+14}{x^2-x-1}\)
\(=x^2-8x+14+\dfrac{\left(a+6\right)x+b+14}{x^2-x-1}\)
Để f(x) chia hết cho g(x) thì a+6=0 và b+14=0
=>a=-6 và b=-14
b: \(\dfrac{f\left(x\right)}{g\left(x\right)}=\dfrac{x^4-x^3+5x^2+x^2-x+5+a-5}{x^2-x+5}\)
\(=x^2+1+\dfrac{a-5}{x^2-x+5}\)
Để f(x) chia hết g(x) thì a-5=0
=>a=5
Đúng 0
Bình luận (0)
Xác định giá trị a,b sao cho đa thức \(Q\left(x\right)=6x^4-7x^3+ax+3x+2\) chia hết cho đa thức \(M\left(x\right)=x^2-x+b\).
Tìm m để đa thức A chia hết cho đa thức B
a)A=\(8x^3-6x^2+3m-4\) B=2x-5
b)A=\(x^3+3x^2+\left(m-8\right)x+m^2-13\) B= \(x^2-x-3\)
bài 3 :
a. Tìm n để đa thức x^4-x^3+6x^2-x+n chia hết cho đa thức x^2-x+5
b. Tìm n để đa thức 3x^3+10x^2-5+n chia hết cho đa thức 3x+1
a) 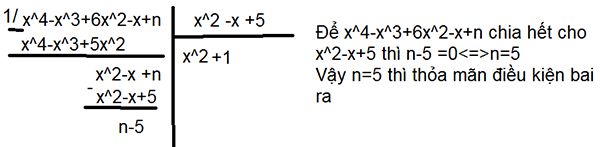
b) 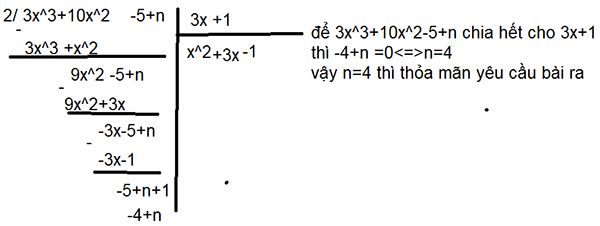
bài 3
a. tìm n để đa thức x^4-x^3+6x^2-x+n chia hết cho đa thức x^2-x+5
b. tìm n để đa thức 3x^3+10x^2-5+n chia hết cho đa thức 3x+1
mk gửi cho link:
https://lazi.vn/edu/exercise/tim-n-de-da-thuc-x4-x3-6x2-x-n-chia-het-cho-da-thuc-x2-x-5
Cho đa thức \(B\left(x\right)=x^4-4x^3-19x^2+106x+m\).Tìm m để B(x) chia hết cho đa thức x^2+2x-5
Bài toán casio trên maytinhbotui.vn
help me !
\(\dfrac{B\left(x\right)}{x^2+2x-5}=\dfrac{x^4-4x^3-19x^2+106x+m}{x^2+2x-5}\)
\(=\dfrac{x^4+2x^3-5x^2-6x^3-12x^2+30x-2x^2-4x+10+80x+m-10}{x^2+2x-5}\)
\(=x^2-6x-2+\dfrac{80x+m-10}{x^2+2x+5}\)
Để đây là phép chia hết thì 80x=-m+10
hay x=-m+10/80
Đúng 0
Bình luận (0)



















