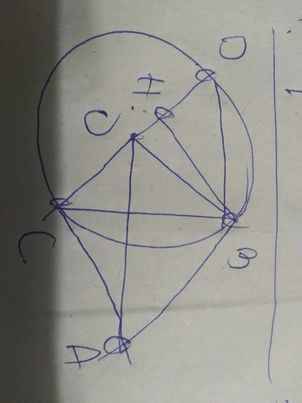
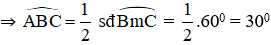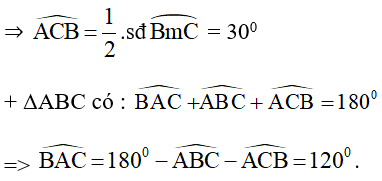Cho đường tròn O bán kính R và dây cung CD=R hai tiếp tuyến của đường tròn (O) tại C và D cắt nhau ở A . tính góc ACD , CAB

Những câu hỏi liên quan
cho đường tròn (o) bán kính R đường kính AB dây cung AC, tiếp tuyến với đường tròn tại B và C cắt nhau ở D
a) CM: DO//AC
b) biết góc BAC = 30 độ bán kính 2 cm tính BD và CD
Cho đường tròn tâm O bán kính R, dây BC khác đường kính, Hai tiếp tuyến của đường tròn (O;R) tại B và tại C cắt nhau tại A. Kẻ đường kính CD, kẻ BH vuông góc với CD tại H.
a) Chứng minh $AO bot BC.$
b) Cho biết $R 15, BC 24 (cm).$ Tính AB, OA.
c) Chứng minh BC là tia phân giác $widehat{ABH}.$
Em cần câu c thôi ạ.
Hình vẽ.
Đọc tiếp
Cho đường tròn tâm O bán kính R, dây BC khác đường kính, Hai tiếp tuyến của đường tròn (O;R) tại B và tại C cắt nhau tại A. Kẻ đường kính CD, kẻ BH vuông góc với CD tại H.
a) Chứng minh $AO \bot BC.$
b) Cho biết $R = 15, BC = 24 (cm).$ Tính AB, OA.
c) Chứng minh BC là tia phân giác $\widehat{ABH}.$
Em cần câu c thôi ạ.
Hình vẽ.
\(ABC\) cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
\(\left\{{}\begin{matrix}\widehat{ACB}+\widehat{BCH}=90^0\\\widehat{CBH}+\widehat{BCH}=90^0\end{matrix}\right.\) \(\Rightarrow\widehat{ACB}=\widehat{CBH}\)
\(\Rightarrow\widehat{ABC}=\widehat{CBH}\)
Đúng 3
Bình luận (2)
Cho đường tròn (O;R) và dây cung BC=R . Hai tiếp tuyến của đường tròn (O) tại B,C cắt nhau ở A . Tính góc ABC và góc BAC
Xét tam giác OBA có OB = OC = BC = R
Vậy tam giác OAB là tam giác đều
=> ^BOC = ^OBC = ^OCB = 600
Vì AB ; AC là tiếp tuyến đường tròn (O) với B;C là tiếp điểm
=> ^OBA = ^OCA = 900
=> ^ABC = ^OBA - ^OBC = 900 - 600 = 300
Do AB = AC ( tc tiếp tuyến cắt nhau )
=> ^ABC = ^ACB = 300
=> ^BAC = 1800 - 2^ABC = 1200
Đúng 1
Bình luận (0)
: Cho đường tròn (O; R) có đường kính AC và dây cung BC R. a) Tính số đo của  và độ dài dây AB theo R. b) Đường thẳng qua O và vuông góc với AB tại H cắt tiếp tuyến tại A của đường tròn (O) ở D. Chứng minh DB là tiếp tuyến của đường tròn (O). c) Vẽ dây BE ⊥ AC tại M . Chứng minh tứ giác OBCE là hình thoi và tính diện tích tứ giác OBCE theo R. d)Tiếp tuyến tại C của (O) cắt DB tại K . Chứng minh AK, CD, BE đồng quy. MK CHỈ CẦN CÂU C THÔI Ạ
Đọc tiếp
: Cho đường tròn (O; R) có đường kính AC và dây cung BC = R. a) Tính số đo của  và độ dài dây AB theo R. b) Đường thẳng qua O và vuông góc với AB tại H cắt tiếp tuyến tại A của đường tròn (O) ở D. Chứng minh DB là tiếp tuyến của đường tròn (O). c) Vẽ dây BE ⊥ AC tại M . Chứng minh tứ giác OBCE là hình thoi và tính diện tích tứ giác OBCE theo R. d)Tiếp tuyến tại C của (O) cắt DB tại K . Chứng minh AK, CD, BE đồng quy. MK CHỈ CẦN CÂU C THÔI Ạ
Cho đường tròn (O; R) đường kính BC và một điểm A nằm trên đường tròn saocho AB R. Gọi H là trung điểm của dây cung AC.a) Tính số đo các góc của tam giác ABC.b) Qua C vẽ tiếp tuyến của đường tròn (O) cắt tia OH tại D. Chứng minh DA là tiếptuyến của đường tròn (O).c) Tính độ dài bán kính của đường tròn ngoại tiếp tam giác ACD theo R.d) Trên tia đối của tia AC lấy điểm M, từ M vẽ hai tiếp tuyến ME và MF với đườngtròn (O) tại E và F. Chứng minh ba điểm D, E, F thẳng hàng.
Đọc tiếp
Cho đường tròn (O; R) đường kính BC và một điểm A nằm trên đường tròn sao
cho AB = R. Gọi H là trung điểm của dây cung AC.
a) Tính số đo các góc của tam giác ABC.
b) Qua C vẽ tiếp tuyến của đường tròn (O) cắt tia OH tại D. Chứng minh DA là tiếp
tuyến của đường tròn (O).
c) Tính độ dài bán kính của đường tròn ngoại tiếp tam giác ACD theo R.
d) Trên tia đối của tia AC lấy điểm M, từ M vẽ hai tiếp tuyến ME và MF với đường
tròn (O) tại E và F. Chứng minh ba điểm D, E, F thẳng hàng.
Cho đường tròn tâm O bán kính R, dây BC khác đường kính. Hai tiếp tuyến của đường tròn ( O,R) tại B và tại C cắt nhau tại A. Kẻ đường tròn CD, kẻ BH vuông góc với CD tại H. A. Chứng minh bốn điểm A,B,O,C cùng thuộc 1 đường tròn. B. chứng minh AO vuông góc với BC. Cho biết R=15cm, BC=24cm. Tính AB,OA. C. Gọi I là giao điểm của AD và BH,E là giao điểm của BC và AC. Chứng minh IH=IB
a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại trung điểm K của BC
K là trung điểm của BC
nên \(KB=KC=\dfrac{BC}{2}=12\left(cm\right)\)
Ta có: ΔBKO vuông tại K
=>\(KB^2+KO^2=OB^2\)
=>\(OK^2=15^2-12^2=81\)
=>\(OK=\sqrt{81}=9\left(cm\right)\)
Xét ΔOBA vuông tại B có BK là đường cao
nên \(OK\cdot OA=OB^2\)
=>\(OA=\dfrac{15^2}{9}=25\left(cm\right)\)
Ta có: ΔOBA vuông tại B
=>\(BO^2+BA^2=OA^2\)
=>\(BA^2=25^2-15^2=400\)
=>\(BA=\sqrt{400}=20\left(cm\right)\)
c: Sửa đề: E là giao điểm của AC và BD
Ta có: BH\(\perp\)CD
AC\(\perp\)CD
Do đó: BH//CD
Xét ΔDCA có HI//CA
nên \(\dfrac{HI}{CA}=\dfrac{DI}{DA}\left(3\right)\)
Xét ΔDAE có IB//AE
nên \(\dfrac{IB}{AE}=\dfrac{DI}{DA}\left(4\right)\)
Xét (O) có
ΔDBC nội tiếp
DC là đường kính
Do đó: ΔDBC vuông tại B
=>DB\(\perp\)BC tại B
=>BC\(\perp\)DE tại B
=>ΔCBE vuông tại B
Ta có: \(\widehat{ABE}+\widehat{ABC}=\widehat{CBE}=90^0\)
\(\widehat{AEB}+\widehat{ACB}=90^0\)(ΔCBE vuông tại B)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABE}=\widehat{AEB}\)
=>AB=AE
mà AB=AC
nên AE=AC
Từ (3) và (4) suy ra \(\dfrac{HI}{CA}=\dfrac{IB}{AE}\)
mà CA=AE
nên HI=IB
Đúng 2
Bình luận (0)
Cho(O;R) đường kính AB và dây cung AC.Các tiếp tuyến với đường tròn tại B và C cắt nhau ở D
a) Cm DO//AC
b) Biết góc BAC=30 độ;R=2cm.Tính BD và CD
a: Xét (O) có
DB là tiếp tuyến
DC là tiếp tuyến
Do đó: DB=DC
hay D nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OD là đường trung trực của BC
hay OD⊥BC(3)
Xét (O) có
ΔACB nội tiếp đường tròn
AB là đường kính
Do đó: ΔACB vuông tại C
hay AC⊥CB(4)
Từ (3) và (4) suy ra AC//OD
Đúng 1
Bình luận (0)
cho đường tròn (O;R) , dây BCneđường kính . 2 tiếp tuyến của đg tròn tại B và C cắt nhau tại A. Kẻ đường kính CD . Kẻ BH vuông góc CD tại Ha, CM: A,B,O,C cùng thuộc 1 đường tròn . Xác định tâm,bán kính đường tròn đób, CM : AO vuông góc BC . Tính AB,OA biết R1,5 và BC24 c, CM: BC là phân giác góc ABHd, I là giao điểm AD và BH , BD giao AC tại E . CM : IHIB
Đọc tiếp
cho đường tròn (O;R) , dây BC\(\ne\)đường kính . 2 tiếp tuyến của đg tròn tại B và C cắt nhau tại A. Kẻ đường kính CD . Kẻ BH vuông góc CD tại H
a, CM: A,B,O,C cùng thuộc 1 đường tròn . Xác định tâm,bán kính đường tròn đó
b, CM : AO vuông góc BC . Tính AB,OA biết R=1,5 và BC=24
c, CM: BC là phân giác góc ABH
d, I là giao điểm AD và BH , BD giao AC tại E . CM : IH=IB
Cho đường tròn (O; R) và dây cung BC = R. Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau tại A. Tính góc ABC và góc BAC
+ ΔOBC có OB = OC = BC (= R)
⇒ ΔOBC là tam giác đều
+ 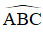
+ 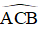
Đúng 3
Bình luận (0)
a) Cho đường tròn tâm O bán kính R. Hai dây AB và CD bằng nhau và vuông gócvới nhau tại I. Chứng minh rằng \(IA^2+IB^2+IC^2+ID^2\) không đổi.b) Trong đường tròn tâm O vẽ dây cung AD không đi qua O. Đường kính vuônggóc với OA cắt tiếp tuyến tại D của (O) tại điểm C. Chứng minh rằng phân giác của gócDCO song song với đường trung trực của AD