Cho tam giác OAB có\(\widehat{O}=120^o\) ,OA= a,OB=b và đường phân giác của O là OC=c. Chứng minh rằng: \(\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{c}\)

Những câu hỏi liên quan
tam giác OAB có góc O =120, OA=a, OB=b, OC là đường phân giác của góc O, OC =c, cmr 1/a+1/b=1/c
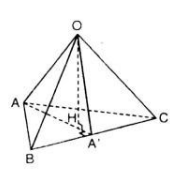
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc. Gọi H là chân đường vuông góc hạ từ O tới mặt phẳng (ABC). Chứng minh rằng :
a) H là trực tâm của tam giác ABC
b) \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}+\dfrac{1}{OC^2}\)
Cho tam giác OAB có góc O=120, OA=a, OB=b. Đường phân giác của góc O là OC=c. CM: 1/a +1/b=1/c
Cho tam giác ABC có 3 cạnh bằng nhau. O là một điểm trong tam giác sao cho OA = OB = OC. Chứng minh rằng O là giao 3 tia phân giác các góc A, B, C của tam giác. (tức là OA là phân giác góc A, OB là phân giác góc B, OC là phân giác góc C)
Ta có AB=AC (GT), AO chung, OB=OC (GT) suy ra tam giác ABO=tam giác ACO (c.c.c)
suy ra góc BAO=góc CAO
mà O là điểm nằm trong tam giác ABC nên tia AO nằm giữa hai tia AB và AC
suy ra AO là tia phân giác của góc BAC (1)
chứng minh tương tự BO là tia phân giác của góc ABC (2)
CO là tia phân giác của góc ACB (3)
Từ(1), (2), (3) suy ra điều phải chứng minh
Cho tam giác OAB có góc O bằng 120o. OC là tia phân giác trong. Chứng minh: 1/OA+1/OB=1/OC
Giúp tôi giải bài toán trên với. Cám ơn nhiều
Kẻ CM // OA, với M thuộc OB
Ta có góc OCM = góc AOC (so le trong) ; góc AOC = góc COM = 600 ( OC là phân giác) => góc OCM = góc COM = 600
Vậy tam giác OCM đều => OC = CM = MO
Ta lại có MC/OA = MB/OB => MC/OA = (OB - OM)/OB => MC/OA = 1 - OM/OB => MC/OA + OM/OB =1
=> OC/OA + OC/OB = 1 hay 1/OA + 1/OB = 1/OC (đpcm)
Đúng 0
Bình luận (0)
Cho ba tia Ox, Oy, Oz tạo thành \(\widehat{xOy}=\widehat{yOz}=60^o\). Một đường thẳng cắt ba tia lần lượt tại A, B, C. Qua B kẻ BB' song song với Oz (B' thuộc tia Ox). Chứng minh:
a) Tam giác OBB' đều
b) \(\dfrac{1}{OB}=\dfrac{1}{OA}+\dfrac{1}{OC}\)
a: góc OBB'=góc BOC=60 độ
=>góc OBB'=góc B'OB=60 độ
=>ΔOBB' đều
b: BB'//OC
=>OB/OC=BB'/OC=AB/AC
OB/OA=OB'/OA=BB'/OA=CB/CA
=>OB/OC+OB/OA=AB/AC+BC/AC=1
=>1/OB=1/OA+1/OC
Đúng 0
Bình luận (0)
Cho tam giác OAB có góc O = 120 độ, OC là đường phân giác trong. CMR: \(\frac{1}{OA}+\frac{1}{OB}=\frac{1}{OC}\)
Cho tam giác ABC có AB = BC = AC. Gọi O là một điểm bất kỳ nằm trong tam giác sao cho OA = OB = OC. Chứng minh rằng O là giao điểm 3 tia phân giác của các góc A; B; C.
Vì OA=OB=OC
nên O là tâm đường tròn ngoại tiếp ΔABC
mà ΔABC đều
nên O là giao điểm của ba tia phân giác của các góc A,B,C
Đúng 1
Bình luận (0)