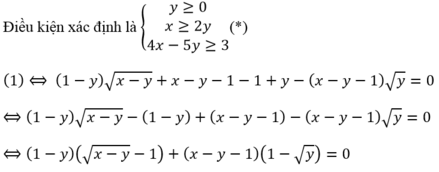tìm nghiệm nguyên dương của phương trình sau:\(yx^2+yx+y=1\)

Những câu hỏi liên quan
Tìm nghiệm nguyên dương của phương trình sau: yx2+yx+y=1
Tìm nghiệm nguyên dương của phương trình sau: yx2 + yx + y = 1
Tìm nghiệm nguyên của phương trình sau:
yx^2+yx+y=1
1. Tìm no nguyên dương của phương trình sau : yx2 + yx + y = 1.
2. Tìm max và min của : A = \(\frac{27-12x}{x^2+9}\)
Cô dì chú bác ơi giúp con với !!!
1, yx2+yx+y=1
=> y(x2+x+1)=1
=>\(y=\frac{1}{x^2+x+1}\)
Vì y là số nguyên dương => 1\(⋮\)x2+x+1
=> x2+x+1=1(vì x>0)
=> vô nghiệm
Vậy không có nghiệm nguyên dương t/m pt
Đúng 0
Bình luận (0)
tìm các cặp (x;y) nguyên dương thoả mãn phương trình yx^3+17(2x-y)^2
Tìm nghiệm nguyên của phương trình: \(yx^2+y=x^3-x^2+2x+7\)
\(y=\frac{x^3-x^2+2x+7}{x^2+1}=x-1+\frac{x+8}{x^2+1}\)
Đặt
\(A=\frac{x+8}{x^2+1}\)
\(\Leftrightarrow\left(x-8\right)A=\frac{x^2-64}{x^2+1}=1-\frac{65}{x^2+1}\)
Để A nguyên thì \(x^2+1\)phải là ước của 65. Làm nốt
Cho hệ sau:
1
-
y
x
-
y
+
x
2
+
x
-...
Đọc tiếp
Cho hệ sau: 1 - y x - y + x = 2 + x - y - 1 y 1 2 y 2 - 3 x + 6 y + 1 = 2 x - 2 y - 4 x - 5 y - 3 2 . Số nghiệm của hệ phương trình là:
A. 0
B. 1
C. 2
D. 3
tìm nghiệm nguyên dương của phương trình sau
xy\(^2\)+yx+y=1
\(\Leftrightarrow x\left(y^2+y\right)=1-y\Leftrightarrow x=\frac{1-y}{y^2+y}\)
Do \(y\) nguyên dương \(\Rightarrow1-y\le0\Rightarrow x\le0\Rightarrow\) không tồn tại nghiệm nguyên dương của pt đã cho
Đúng 0
Bình luận (0)
Bài tập:
a) Tìm nghiệm nguyên dương của phương trình sau: \(yx^2+yx+y=1\)
b) Tìm GTLN của biểu thức: \(B=\dfrac{x^2}{1+x^4}\) với \(x\ne0\)
Ta có:
\(B=\dfrac{x^2}{x^4+1}\)
\(2B-1=\dfrac{2x^2-x^4-1}{x^4+1}\)
\(2B-1=\dfrac{-\left(x^2-1\right)^2}{x^4+1}\)
Ta có:
\(\dfrac{-\left(x^2-1\right)}{x^4+1}\le0\)
\(\Rightarrow2B-1\le0\)
\(\Leftrightarrow B\le\dfrac{1}{2}\)
dấu "=" xảy ra khi
\(x^2=1\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Đúng 0
Bình luận (2)