Tìm a,b để P(x)= ax2013+ bx2014+ 3x+ b chia hết cho đa thức (x2-1)

Những câu hỏi liên quan
Tìm hai số thực a và b để đa thức ax3 +x2-x+b chia hết cho đa thức x2+3x+2.
- Để hai đa thức trên chia cho nhau hết thì :\(\left\{{}\begin{matrix}7a-4=0\\b-2\left(1-3a\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7a=4\\6a+b=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{4}{7}\\b=-\dfrac{10}{7}\end{matrix}\right.\)
Vậy ...
Đúng 2
Bình luận (1)
b) Thực hiện phép chia đa thức (2x4 – 5x3 + 2x2 +2x - 1) cho đa thức (x2 – x - 1)
Bài 2:
a) Tìm a để đa thức (2x4 + x3 - 3x2 + 5x + a) chia hết cho đa thức (x2 - x +1)
b) Tìm a để đa thức x^4 - x^3 + 6x^2 chia hết cho đa thức x^2 - x + 5
b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)
Đúng 0
Bình luận (0)
Tìm a và b để đa thức A chia hết cho đa thức B với:a) A
4
x
3
+
15
x
2
+ 24x + 3 + a và B
x
2
+ 4x + 7;b) A
x
4
+
3
x
3
-
x
2
+ (2a - 3)x +...
Đọc tiếp
Tìm a và b để đa thức A chia hết cho đa thức B với:
a) A = 4 x 3 + 15 x 2 + 24x + 3 + a và B = x 2 + 4x + 7;
b) A = x 4 + 3 x 3 - x 2 + (2a - 3)x + 3b + a và B = x 2 + 3x - 1.
Tìm các số nguyên a và b để đa thức A(x)=x4-3x3+ax +b chia hết cho đa thức
B(x)=x2-3x+4
bạn trúc giang sai rồi -4 nhân -3x sao lại bằng -12x
Đúng 0
Bình luận (0)
Tìm a, b để đa thức A ( x ) = 2 x 3 – x 2 + a x + b chia hết cho đa thức B ( x ) = x 2 – 1
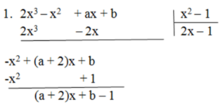
A(x) chia hết cho B(x) khi (a + 2)x + b – 1 là đa thức 0
Vậy a + 2 = 0 và b – 1 = 0 ⇒ a = -2 và b = 1
Đúng 1
Bình luận (0)
Tìm a, b để đa thức
A
(
x
)
2
x
3
–
x
2
+
a
x
+
b
chia hết cho đa thức
B
(
x
)
x
2
–
1
Đọc tiếp
Tìm a, b để đa thức A ( x ) = 2 x 3 – x 2 + a x + b chia hết cho đa thức B ( x ) = x 2 – 1
Tìm a, b để đa thức
A
(
x
)
2
x
3
–
x
2
+
a
x
+
b
chia hết cho đa thức
B
(
x
)
x
2
–
1
Đọc tiếp
Tìm a, b để đa thức A ( x ) = 2 x 3 – x 2 + a x + b chia hết cho đa thức B ( x ) = x 2 – 1
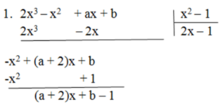
A(x) chia hết cho B(x) khi (a + 2)x + b – 1 là đa thức 0
Vậy a + 2 = 0 và b – 1 = 0 ⇒ a = -2 và b = 1
Đúng 0
Bình luận (0)
tìm x nguyên để giá trị của đa thức A chia hết cho giá trị của đa thức B.
a) A = -2x3-3x2+12x+2 và B =2x-1
b) A =-3x3+x2+15x-6 và B =3x+1
Tìm a để đa thức: X²+X²+A-X chia hết cho (X+1)².
Tìm m để đa thức A(x)=x³-3x²+5x+m chia hết cho đa thức B(x)=x-2
Tìm n € Z để 2n²-n+2 chia hết cho n+1
a) đề x3+x2-x +a chia hét cho (x-1)2 ?
x3+x2-x +a=x(x2-2x+1)+3(x2-2x+1)+4x-3+a đề sai nhé
b)A(2)=0=> 8-12+10+m=0 => m=6
c)2n2-n+2=2n(n+1)-3(n+1) +5 chia het cho n+1 khi n+1 là ước của 5
n+1=-1;1;-5;5
n=-2;0;-6;4
Đúng 0
Bình luận (0)
Cho đa thức A(x) = 1 + x2 + x4 + .... + x2n - 2; B= 1 + x + x2 + ... + xn-1. Tìm số nguyên dương n để đa thức A(x) chia hết cho đa thức B(x).
A(x)=(1-x^n)(1+x^n)/(1-x)(1+x)
B(x)=1-x^n/1-x
A(x) chia hết cho B(x) khi 1-x^n chia hết cho 1+x
x^n+1/x+1=A(x)+(1+(-1)^n)/(x+1)
=>1-x^n chia hết cho 1+x khi và chỉ khi n=2k+1
Đúng 1
Bình luận (1)



















