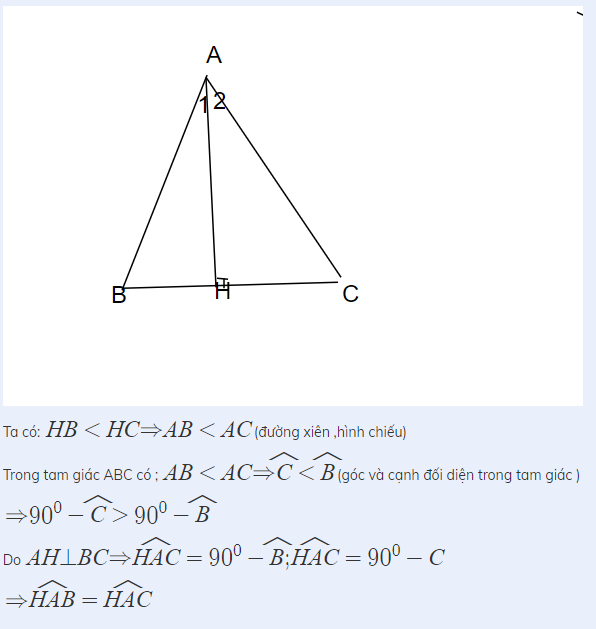
Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC .Biết HB <HC.
CMR : \(\widehat{AHB}=\widehat{HAC}\)
câu 1 Cho tam giác ABC có các góc B, C nhọn. Kẻ AH vuông góc với BC. Biết AB = 20cm, BH = 16cm, HC = 5cm. Tính AH, AC.
câu 2 Cho tam giác ABC có các góc B, C nhọn. Kẻ AH vuông góc với BC, biết AC = 15cm, HB = 5cm, HC = 9cm . Tính độ dài cạnh AB.
Câu 1:
Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
202 = AH2 + 162
400 = AH2 + 256
AH2 = 400 - 256
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
AC2 = 122 + 52
AC2 = 144 + 25
AC2 = 169
AC = \(\sqrt{169}\)= 13 (cm)
Vậy AH = 12 cm
AC = 13 cm
Bài 2:
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
152 = AH2 + 92
225 = AH2 + 81
AH2 = 225 - 81
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHB vuông tại, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = \(\sqrt{169}\)= 13 (cm)
Vậy AB = 13 cm
Cho tam giác tam giác ABC có 3 góc nhọn kẻ AH vuông góc BC(H thuộc BC).Biết HB<HC. CMR: góc HAB<góc HAC
tham khảo tại: https://olm.vn/hoi-dap/detail/215686516317.html
Cho tam giác ABC có 3 góc nhọn,kẻ AH vuông góc với BC ,biết HB < HC .CMR :góc HAB < góc HAC
Bài 3: Cho tam giác ABC nhọn. Kẻ AH vuông góc với BC. Biết AC = 20cm; AH = 12cm; HB = 5cm a/ Tính độ dài cạnh AB b/ Tính chu vi tam giác ABC
a) Xét ΔAHB vuông tại H áp dụng định lý Py-ta-go ta có:
\(AB^2=AH^2+HB^2\)
\(\Rightarrow AB=\sqrt{AH^2+HB^2}\)
\(\Rightarrow AB=\sqrt{12^2+5^2}=13\left(cm\right)\)
b) Xét ΔAHC vuông tại H áp dụng định lý Py-ta-go ta có:
\(AC^2=AH^2+HC^2\)
\(\Rightarrow HC=\sqrt{AC^2-AH^2}\)
\(\Rightarrow HC=\sqrt{20^2-12^2}=16\left(cm\right)\)
\(\Rightarrow BC=HB+HC=5+16=21\left(cm\right)\)
\(\Rightarrow C_{ABC}=BC+AB+AC=21+13+20=54\left(cm\right)\)
cho tam giác ABC nhọn , kẻ AH vuông góc với BC (H thuộc BC ) . cho biết AC = 20cm , AH = 12cm , BH=5cm . tính độ dài cạnh HB , HBC
Giúp mình với !!! vẽ hình giúp mình với nha !! ![]()
Bài 1: Cho tam giác ABC vuông tại A. Biết BC = 41cm; AC = 40cm. Tính
a) Độ dài cạnh AB
b) Chu vi tam giác ABC
Bài 2: Cho tam giác ABC nhọn. Kẻ AH vuông góc với BC. Biết AC = 20cm; AH =
12cm; HB = 5cm
a) Tính độ dài cạnh AB
b) Tính chu vi tam giác ABC
Bài 3: Cho tam giác ABC có BC = 10cm , AB = 6cm và AC = 8cm . Tam giác ABC là
tam giác gì ? Vì sao ?
Bài 4: Cho tam giác ABC vuông tại A, có B 60 0 và AB = 5cm. Tia phân giác của góc
B cắt AC tại D. Kẻ DE vuông góc với BC (EBC) . Chứng minh:
a) ABD = EBD.
b) ABE là tam giác đều.
c) AEC cân.
d) Tính độ dài cạnh AC.
Bài 5: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC ( HBC )
a) Chứng minh: AHB = AHC
b) Giả sử AB = AC = 5cm, BC = 8cm. Tính độ dài AH
c) Trên tia đối của tia HA lấy điểm M sao cho HM = HA. Chứng minh ABM
cân
d) Chứng minh BM // AC
Bài 6: Cho tam giác ABC vuông tại A, phân giác BE. Kẻ EK vuông góc với BC tại K.
Gọi M là giao điểm của BA và KE. Chứng minh :
a) ΔABE = ΔKBE
b) EM = EC
c) AK // MC
d) So sánh AE và EC
e) Gọi N là trung điểm của MC. Chứng minh 3 điểm B, E, N thẳng hàng
Bài 7: Cho ABC có AB = AC =10cm, BC = 12cm. Vẽ AH vuông góc BC tại H.
a) Chứng minh: ABC cân.
b) Chứng minh AHB AHC, từ đó chứng minh AH là tia phân giác của góc
A.
c) Từ H vẽ HM AB ( ) M AB và kẻ HN AC ( ) N AC . C/m: BHM = HCN
d) Tính độ dài AH.
e) Từ B kẻ Bx AB, từ C kẻ Cy AC chúng cắt nhau tại O. Tam giác OBC là
tam giác gì? Vì sao?
bạn đăng tách ra nhé
Bài 1 :
Theo định lí Pytago tam giác ABC vuông tại A
\(AB=\sqrt{BC^2-AC^2}=9cm\)
Chu vi tam giác ABC là 41 + 40 + 9 = 90 cm
Bài 4: Cho tam giác ABC có ba góc nhọn , kẻ AH vuông góc với cạnh BC. Biết HB < HC , chứng minh rằng ; ^HAB < ^HAC
ta có BAHˆ=AHCˆ=AHBˆ=90BAH^=AHC^=AHB^=90
BAHˆ=ACBˆBAH^=ACB^ ( cùng phụ HACˆHAC^)
HACˆ=ABCˆHAC^=ABC^( cùng phụ BAHˆBAH^)
Giải:
Có: HB < HC
Mà HB là hình chiếu của AB lên BC
HC là hình chiếu của AC lên BC
=> AB < AC ( mối quan hệ đường xiên và hình chiếu )
=> ^C < ^B => ^C - ^B < 0 (1)
Vì \(\Delta\)ABH vuông tại B => ^B + ^HAB = 90 độ
\(\Delta\)ACH vuông tại C => ^C + ^HAC = 90 độ
=> ^HAB + ^B = ^C + ^HAC
=> ^HAB - ^HAC = ^C - ^B < 0 ( theo (1))
=> ^HAB < ^HAC.
cho tam giác ABC nhọn kẻ AH vuông góc với BC biết AC=20cm AH = 12cm , HB = 5cm
a, tính độ dài cạnh AB
b, tính chu vi tam giác ABC
Áp dụng định lý Pi ta go vào tam giác AHB ,có:
\(AB=\sqrt{AH^2+HB^2}=\sqrt{12^2+5^2}=13\left(cm\right)\)
Áp dụng định lý Pi ta go vào tam giác AHC ,có:
\(HC=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=16\left(cm\right)\)
Chu vi tam giác ABC là:
\(13+20+5+16=54\left(cm\right)\)
=54 nha
HT
k cho mình nha
@@@@@@@@@@@@@@@@@@
Cho tam giác ABC có các góc B,C nhọn. Kẻ AH vuông góc với BC biết AC=15cm;HB=5cm;HC=17cm. Tính AB
Cho Tam giác abc có 3 góc nhọn, kẻ AH vuông góc BC tại H, biết rằng HC lớn hơn HB. Chứng minh:AC lớn hơn AB
+Vì HC>HB nên đáy tam giác AHC> đáy tam giác AHB
Dựa vào định lý Pi-ta-go,ta có:
\(AH^2+CH^2=AC^2\); \(AH^2+HB^2=AB^2\)
Mà AC>AB nên \(AC^2>AB^2\)
Vậy AC>AB
áp dụng định lí Py-ta-go cho tam giác ABH vuông tại H ta có: AB2=AH2+BH2
áp dụng định lí Py-ta-go cho tam giác ACH vuông tại h ta có: AC2=AH2+CH2
mà CH>BH nên CH2>BH2
=>AH2+CH2>AH2+BH2=> AC2>AB2 => AC>AB => dpcm