Giải phương trình sau:
(3x2+x-2016)2+4(x2+506x-2017)2=4(3x2+x-2016).(x2+506x-2017)
a)giải phương trình sau
\(\left(3x^2+x-2016\right)^2+4\left(x^2+506x-2017\right)^2=4\left(3x^2+x-2016\right).\left(x^2+506x-2017\right)\)
b) tìm đa thức f(x) biết rằng f(x) chia cho x+3 duw, f(x) chia cho x-2duw 6, f(x) chia cho x2+x-6 được thương là 2x và còm dư
a)giải phương trình sau
\(\left(3x^2+x-2016\right)^2+4\left(x^2+506x-2017\right)^2=4\left(3x^2+x-2016\right).\left(x^2+506x-2017\right)\)
b) tìm đa thức f(x) biết rằng f(x) chia cho x+3 duw, f(x) chia cho x-2duw 6, f(x) chia cho x2+x-6 được thương là 2x và còm dư
a)\(\left(3x^2+x-2016\right)^2+4\left(x^2+506x-2017\right)^2=4\left(3x^2+x-2016\right)\cdot\left(x^2+506x-2017\right)\)
\(\Leftrightarrow\left(3x^2+x-2016\right)^2-4\left(3x^2+x-2016\right)\left(x^2+506x-2017\right)+4\left(x^2+506x-2017\right)^2=0\)
\(\Leftrightarrow\left(3x^2+x-2016-2x^2-1012x+4034\right)^2=0\)
\(\Leftrightarrow x^2-1011x+2018=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1009\end{matrix}\right.\)
Giải bất phương trình sau: x 2 + x - 3 x 2 - 4 ≥ 1
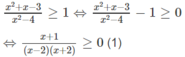
Bảng xét dấu vế trái của (1)
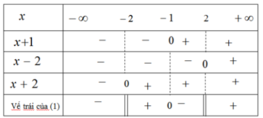
Đáp số: -2 < x ≤ -1, x > 2
Giải phương trình (2x^2 +x -2017)^2 + 4(x^2 -5x-2016)^2=4(2x^2+x-2017)(x^2-5x-2016)
\(\Leftrightarrow\left(2x^2+x-2017\right)^2-4\left(2x^2+x-2017\right)\left(x^2-5x-2016\right)+4\left(x^2-5x-2016\right)^2=0\)
\(\Leftrightarrow\left(2x^2+x-2017-2\left(x^2-5x-2016\right)\right)^2=0\)
\(\Leftrightarrow11x-6049=0\)
\(\Rightarrow x=\frac{6049}{11}\)
Giải các phương trình sau:
a) x + 3 3 − x − 1 3 = 0 ;
b) x 4 + x 2 − 2 = 0 ;
c) x 3 + 3 x 2 + 6 x + 4 = 0 ;
d) x 3 − 6 x 2 + 8 x = 0 .
a) Cách 1: Khai triển HĐT rút gọn được 3 x 2 + 6x + 7 = 0
Vì (3( x 2 + 2x + 1) + 4 < 0 với mọi x nên giải được x ∈ ∅
Cách 2. Chuyển vế đưa về ( x + 3 ) 3 = ( x - 1 ) 3 Û x + 3 = x - 1
Từ đó tìm được x ∈ ∅
b) Đặt x 2 = t với t ≥ 0 ta được t 2 + t - 2 = 0
Giải ra ta được t = 1 (TM) hoặc t = -2 (KTM)
Từ đó tìm được x = ± 1
c) Biến đổi được ![]()
d) Biến đổi về dạng x(x - 2) (x - 4) = 0. Tìm được x ∈ {0; 2; 4}
Câu 1 : Phương trình nào trong các phương trình dưới đây là phương trình bậc nhất ?
A. 7 - x - 3x2 = x - 3x2 B. 4 - x = - ( x - 1)
C. 3 - x + x2 = x2 - x - 2 D. ( x - 3 )( x + 5 ) = 0
Câu 2 : Phương trình nào dưới đây có tập nghiệm là S = {3; -1}
A. ( x + 3)(x - 1) = 0 B. x2 + 3x + 2 = 0
C. x( x – 3)(x + 1)2 = 0 D. ( x – 3)(x + 1) = 0
Câu 3 : Phương trình nào dưới đây có vô số nghiệm ?
A. ( x + 3 )( x2 + 5 ) = 0. B. x2 = - 9
C. x3 = - 27 D. 5x - 3 + 3x = 8x - 3
Câu 4 : Phương trình - 2x2 + 11x - 15 = 0 có tập nghiệm là:
A. 3 B. C . D.
Câu 5. Điều kiện xác định của phương trình là:
A hoặc x ≠ -3 B.; C. và x ≠ - 3; D. x ≠ -3
Câu 6. Biết và CD = 21 cm. Độ dài của AB là:
A. 6 cm B. 7 cm; C. 9 cm; D. 10 cm
Câu 7. Cho tam giác ABC, AM là phân giác (hình 1). Độ dài đoạn thẳng MB bằng:
A. 1,7 B. 2,8 C. 3,8 D. 5,1
Câu 8. Trong Hình 2 biết MM' // NN', MN = 4cm, OM’ = 12cm và M’N’ = 8cm. Số đo của đoạn thẳng OM là:
A. 6cm; B. 8cm; C. 10cm; D. 5cm
Hình 1 Hình
1.B
2.D
3.B
4;5;6;7;8( bạn sửa lại đề nhé )
Giải các phương trình sau:
a) 2 x + 1 2 − 2 x − 1 = 2 ;
b) x 2 − 3 x 2 + 5 x 2 − 3 x + 6 = 0 ;
c) x 2 − x − 1 x 2 − x − 2 = 0 .
Giải phương trình nghiệm nguyên
a) \(x^2+6x+17^{91}=2016^{2020}\)
b) \(x^2+2017^{2019}=2016\left(y-1\right)^2\)
c) \(x^2-2x=2017^{2017}\)
d) \(x^2+4x=2018^{10}\)
Lời giải:
a.
PT $\Leftrightarrow (x+3)^2=2016^{2020}-17^{91}+9$
Ta thấy: $2016^{2020}-17^{91}+9\equiv 0-(-1)^{91}+0\equiv -1\equiv 2\pmod 3$
Mà 1 scp thì chia $3$ chỉ dư $0$ hoặc $1$ nên pt vô nghiệm.
b.
$x^2=2016(y-1)^2-2017^{2019}\equiv 0-1^{2019}\equiv 3\pmod 4$
Mà 1 scp chia $4$ chỉ dư $0$ hoặc $1$ nên vô lý.
Vậy pt vô nghiệm.
c.
$(x-1)^2=2017^{2017}+1\equiv 1^{2017}+1\equiv 2\pmod 4$
Mà 1 scp khi chia cho $4$ chỉ dư $0$ hoặc $1$ nên vô lý
Vậy pt vô nghiệm
d.
$(x+2)^2=2018^{10}+4\equiv (-1)^{10}+1\equiv 2\pmod 3$
Mà 1 scp khi chia $3$ dư $0$ hoặc $1$ nên vô lý
Vậy pt vô nghiệm.
Giải bất phương trình sau:
a) 3x2 - 10x - 8 > 0
b) x2 + (x + 2)(11 - 7x) > 12
c) 3x - 4/x + 2 ≥ 4
d) x2 - x/1 + x2 ≤ 1
e) x/1 - 2x > x2 - x - 1/1 - 4x2
Giúp mik vs mọi người ơi mai mik ktra rồi THANKS TRƯỚC NHA!