khó quá . bó tay .com .vn 

khó qá

mà các bn mai đi học à?

tụi mik chỉ lên khai giảng rồi về thôi =))

kho qua

ban dua cau hoi nay len 24h nha

ĐK: \(x\ge\frac{1}{3}\)

Pt đã cho tương đương với \(\left(18x^2-2x-\frac{8}{3}\right)+9\left(\sqrt{x-\frac{1}{3}}-\frac{1}{3}\right)=0\)

\(\Leftrightarrow\left(18x-8\right)\left(x+\frac{1}{3}\right)+9\frac{x-\frac{1}{3}-\frac{1}{9}}{\sqrt{x-\frac{1}{3}}+\frac{1}{3}}=0\)

\(\Leftrightarrow\left(x-\frac{4}{9}\right)\text{[}18\left(x+\frac{1}{3}\right)+9\frac{1}{\sqrt{x-\frac{1}{3}}+\frac{1}{2}}\text{]}=0\Rightarrow x=\frac{4}{9}\)

CM: Với \(x\ge\frac{1}{3}\Rightarrow18\left(x+\frac{1}{3}\right)+9\frac{1}{\sqrt{x-\frac{1}{3}}+\frac{1}{3}}>0\)

Pt đã cho có nghiệm \(x=\frac{4}{9}\)

\(a,ĐK:x\ge1\\ PT\Leftrightarrow\sqrt{x-1}+2\sqrt{x-1}-5\sqrt{x-1}=-2\\ \Leftrightarrow-2\sqrt{x-1}=-2\Leftrightarrow\sqrt{x-1}=1\\ \Leftrightarrow x-1=1\Leftrightarrow x=2\left(tm\right)\\ b,ĐK:x\ge0\\ PT\Leftrightarrow\dfrac{1}{3}\sqrt{2x}-2\sqrt{2x}+3\sqrt{2x}=12\\ \Leftrightarrow\dfrac{4}{3}\sqrt{2x}=12\Leftrightarrow\sqrt{2x}=9\\ \Leftrightarrow2x=81\Leftrightarrow x=\dfrac{81}{2}\left(tm\right)\)

a) \(x-\left(5x+3\right)=2x-4\)

\(\Leftrightarrow x-5x-3=2x-4\)

\(\Leftrightarrow x-5x-2x=-4+3\)

\(\Leftrightarrow-6x=-1\)

\(\Leftrightarrow x=\frac{1}{6}\)

b) \(2x^3-18x=0\)

\(\Leftrightarrow2x\left(x^2-9\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}2x=0\\x^2-9=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm3\end{cases}}\)

c)\(\left(x-3\right)^2=\left(2x+7\right)^2\)

\(\Leftrightarrow x-3=2x+7\)

\(\Leftrightarrow x-2x=7+3\)

\(\Leftrightarrow-x=10\)

\(\Leftrightarrow x=-10\)

a) 2(x + 3)(x – 4) = (2x – 1)(x + 2) – 27

⇔ 2(x2 – 4x + 3x – 12) = 2x2 + 4x – x – 2 – 27

⇔ 2x2 – 2x – 24 = 2x2 + 3x – 29

⇔ -2x – 3x = 24 – 29

⇔ - 5x = - 5 ⇔ x = -5/-5 ⇔ x = 1

Tập nghiệm của phương trình : S = {1}

b) x2 – 4 – (x + 5)(2 – x) = 0

⇔ x2 – 4 + (x + 5)(x – 2) = 0 ⇔ (x – 2)(x + 2 + x + 5) = 0

⇔ (x – 2)(2x + 7) = 0 ⇔ x – 2 = 0 hoặc 2x + 7 = 0

⇔ x = 2 hoặc x = -7/2

Tập nghiệm của phương trình: S = {2; -7/2 }

c) ĐKXĐ : x – 2 ≠ 0 và x + 2 ≠ 0 (khi đó : x2 – 4 = (x – 2)(x + 2) ≠ 0)

⇔ x ≠ 2 và x ≠ -2

Quy đồng mẫu thức hai vế :

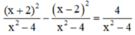
Khử mẫu, ta được : x2 + 4x + 4 – x2 + 4x – 4 = 4

⇔ 8x = 4 ⇔ x = 1/2( thỏa mãn ĐKXĐ)

Tập nghiệm của phương trình : S = {1/2}

d) ĐKXĐ : x – 1 ≠ 0 và x + 3 ≠ 0 (khi đó : x2 + 2x – 3 = (x – 1)(x + 3) ≠ 0)

⇔ x ≠ 1 và x ≠ -3

Quy đồng mẫu thức hai vế :

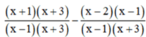
Khử mẫu, ta được : x2 + 3x + x + 3 – x2 + x – 2x + 2 + 4 = 0

⇔ 3x = -9 ⇔ x = -3 (không thỏa mãn ĐKXĐ)

Tập nghiệm của phương trình : S = ∅

\(2\left(x+3\right)\left(x-4\right)=\left(2x-1\right)\left(x+2\right)-27\)

\(< =>2\left(x^2-x-12\right)=2x^2+3x-2-27\)

\(< =>2x^2-2x-24=2x^2+3x-2-27\)

\(< =>5x=-24+29=5\)

\(< =>x=\frac{5}{5}=1\)

\(x^2-4-\left(x+5\right)\left(2-x\right)=0\)

\(< =>\left(x-2\right)\left(x+2\right)+\left(x+5\right)\left(x-2\right)=0\)

\(< =>\left(x-2\right)\left(x+2+x+5\right)=0\)

\(< =>\left(x-2\right)\left(2x+7\right)=0\)

\(< =>\orbr{\begin{cases}x-2=0\\2x+7=0\end{cases}}< =>\orbr{\begin{cases}x=2\\x=-\frac{7}{2}\end{cases}}\)