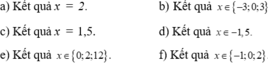\(a,PT\Leftrightarrow x^3-6x^2+12x-8-x^3+x+6x^2-18x-10=0\)

\(\Leftrightarrow-5x-18=0\)

\(\Leftrightarrow x=-\dfrac{18}{5}\)

Vậy ...

\(b,PT\Leftrightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1-6x^2+12x-6+10=0\)

\(\Leftrightarrow12x+6=0\)

\(\Leftrightarrow x=-\dfrac{1}{2}\)

Vậy ...

\(c,PT\Leftrightarrow\left(x+1\right)^3+3^3=0\)

\(\Leftrightarrow\left(x+1+3\right)\left(x^2+2x+1-3x-3+9\right)=0\)

\(\Leftrightarrow\left(x+4\right)\left(x^2-x+7\right)=0\)

Thấy : \(x^2-\dfrac{2.x.1}{2}+\dfrac{1}{4}+\dfrac{27}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{27}{4}\ge\dfrac{27}{4}>0\)

\(\Rightarrow x+4=0\)

\(\Leftrightarrow x=-4\)

Vậy ...

\(d,PT\Leftrightarrow\left(x-2\right)^3+1^3=0\)

\(\Leftrightarrow\left(x-2+1\right)\left(x^2-4x+4-x+2+1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(x^2-5x+7\right)=0\)

Thấy : \(x^2-5x+7=x^2-\dfrac{5.x.2}{2}+\dfrac{25}{4}+\dfrac{3}{4}=\left(x-\dfrac{5}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\)

\(\Rightarrow x-1=0\)

\(\Leftrightarrow x=1\)

Vậy ...

a) x = 0                 b) x = - 1 3

c) x = 28 15               d) x = -82.

Câu 1:

b: ĐKXĐ: \(x\notin\left\{3;-3\right\}\)

\(\dfrac{1}{x-3}-\dfrac{1}{x+3}+\dfrac{2x}{9-x^2}\)

\(=\dfrac{1}{x-3}-\dfrac{1}{x+3}-\dfrac{2x}{\left(x-3\right)\left(x+3\right)}\)

\(=\dfrac{x+3-x+3-2x}{\left(x-3\right)\left(x+3\right)}=\dfrac{-2x+6}{\left(x-3\right)\left(x+3\right)}\)

\(=\dfrac{-2\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=-\dfrac{2}{x+3}\)

c: ĐKXĐ: \(x\notin\left\{2;0\right\}\)

Sửa đề: \(\dfrac{x+1}{x-2}+\dfrac{4-5x}{x^3+4x}:\dfrac{x-2}{x^2+4}\)

\(=\dfrac{x+1}{x-2}+\dfrac{4-5x}{x\left(x^2+4\right)}\cdot\dfrac{x^2+4}{x-2}\)

\(=\dfrac{x+1}{x-2}+\dfrac{4-5x}{x\left(x-2\right)}\)

\(=\dfrac{x\left(x+1\right)+4-5x}{x\left(x-2\right)}=\dfrac{x^2+x-5x+4}{x\left(x-2\right)}\)

\(=\dfrac{x^2-4x+4}{x\left(x-2\right)}=\dfrac{\left(x-2\right)^2}{x\left(x-2\right)}=\dfrac{x-2}{x}\)

1) ĐKXĐ: \(x\notin\left\{-2;2\right\}\)

Ta có: \(\dfrac{x-1}{x+2}-\dfrac{9}{x^2-4}=\dfrac{-3}{x-2}\)

\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}-\dfrac{9}{\left(x-2\right)\left(x+2\right)}=\dfrac{-3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\)

Suy ra: \(x^2-3x+2-9=-3x-6\)

\(\Leftrightarrow x^2-3x-7+3x+6=0\)

\(\Leftrightarrow x^2-1=0\)

\(\Leftrightarrow\left(x-1\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)

Vậy: S={1;-1}

2)

Sửa đề: \(\dfrac{3x-3}{x^2-9}-\dfrac{1}{x-3}=\dfrac{x+1}{x+3}\)

ĐKXĐ: \(x\notin\left\{3;-3\right\}\)

Ta có: \(\dfrac{3x-3}{x^2-9}-\dfrac{1}{x-3}=\dfrac{x+1}{x+3}\)

\(\Leftrightarrow\dfrac{3x-3}{\left(x-3\right)\left(x+3\right)}-\dfrac{x+3}{\left(x-3\right)\left(x+3\right)}=\dfrac{\left(x+1\right)\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}\)

Suy ra: \(3x-3-x-3=x^2-3x+x-3\)

\(\Leftrightarrow x^2-2x-3=2x-6\)

\(\Leftrightarrow x^2-2x-3-2x+6=0\)

\(\Leftrightarrow x^2-4x+3=0\)

\(\Leftrightarrow x^2-x-3x+3=0\)

\(\Leftrightarrow x\left(x-1\right)-3\left(x-1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(x-3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\x=3\left(loại\right)\end{matrix}\right.\)

Vậy: S={1}

`1)(x-1)/(x+2)-9/(x^2-4)=-3/(x-2)(x ne 2)`

`<=>x^2-3x+2-9=-3x-6`

`<=>x^2-1=0`

`<=>x=+-1`

a) \(x^3+2\left(x-1\right)^2-2\left(x-1\right)\left(x+1\right)=x^3+x-4-\left(x-7\right)\).

\(\Leftrightarrow x^3+2\left(x^2-2x+1\right)-2\left(x^2-1\right)=x^3+x-4-x+7\)

\(\Leftrightarrow x^3+2x^2-4x+2-2x^2+2=x^3+3\)

\(\Leftrightarrow x^3-4x+4=x^3+3\)

\(\Leftrightarrow4x-1=0\)

\(\Leftrightarrow x=\frac{1}{4}\)

Vậy tập nghiệm của phương trình là \(S=\left\{\frac{1}{4}\right\}\)

b) \(2\left(x-3\right)+1=2\left(x+1\right)-9\)

\(\Leftrightarrow2x-6+1=2x+2-9\)

\(\Leftrightarrow2x-5=2x-7\)

\(\Leftrightarrow2=0\)(ktm)

Vậy tập nghiệm của phương trình là \(S=\varnothing\)

c) \(3\left(x+1\right)\left(x-1\right)-5=3x^2+2\)

\(\Leftrightarrow3\left(x^2-1\right)-5=3x^2+2\)

\(\Leftrightarrow3x^2-3-5=3x^2+2\)

\(\Leftrightarrow3x^2-8=3x^2+2\)

\(\Leftrightarrow0=10\)(ktm)

Vậy tập nghiệm của phương trình là \(S=\varnothing\)

a: (1-2x)^3-(1+2x)^3

\(=1^3-3\cdot1^2\cdot2x+3\cdot1\cdot\left(2x\right)^2-8x^3-8x^3-12x^2-6x-1\)

\(=1-6x+12x^2-8x^3-8x^3-12x^2-6x-1\)

\(=-16x^3-12x\)

b: \(=x^3-6x^2+12x-8-x^3-x^2+8\)

\(=-7x^2+12x\)

c: \(=x^3+8-12x+6x^2-x^3+6x^2+12x\)

\(=12x^2+8\)

1: \(=x^2+1\)

3: \(=\left(x-y-z\right)^2\)