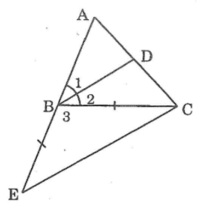
Ta có: BD là tia phân giác của ∠ABC (giả thiết)

Suy ra: 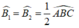 (1)

Lại có: BE = BC (giả thiết)

=>∆BEC cân tại B (theo định nghĩa)

Suy ra: ∠E= ∠BCE (tính chất tam giác cân)

∆BEC có ABC là góc ngoài đỉnh B

=>∠ABC= ∠E + ∠BCE (tính chất góc ngoài tam giác)

Suy ra: ∠ABC=2∠E

Hay ∠E = (1/2)∠ABC (2)

Từ (1) và (2) suy ra: ∠E = ∠B1 = (1/2)∠ABC

Vậy BD // CE (vì có cặp góc ở vị trí đồng vị bằng nhau)

Tham khảo : Câu hỏi của Min Anna - Toán lớp 7 | Học trực tuyến

Ta có: BD là tia phân giác của \(\widehat{ABC}\left(gt\right)\)

\(\Rightarrow B_1=B_2=\left(\frac{1}{2}\right)ABC\)

Lại có :  BE = BC (gt) 

=>∆BEC cân tại B (theo định nghĩa)

\(\widehat{E}=\widehat{BCE}\) (tính chất tam giác cân)

\(\Delta BEC\) có ABC là ngoài đỉnh B 

\(\Rightarrow\widehat{ABC}=\widehat{E}+\widehat{BCE}\) (tính chất góc ngoài tam giác)

\(\Rightarrow\widehat{ABC}=2\widehat{E}\)

Hay \(\widehat{E}=\widehat{B_1}=\left(\frac{1}{2}\right)\widehat{ABC}\)

Vậy BD // CE (vì có cặp góc ở vị trí đồng vị bằng nhau)

Chúc bạn học tốt !!!

Tự vẽ hình nha bn !

Ta có : ΔEBC cân B ( Vì BE=BC)
=> góc BEC = góc BCE ( Tam giác cân có hai góc ở đáy = nhau
mà góc BEC + góc BCE = góc ABC = 180 độ (t/c góc ngoài của Δ)
Ta lại có góc ABD = góc CBD (BD là tia p/g góc ABC)
=> 2 góc BEC = 2 góc CBD
=> góc BEC = góc CBD
mà 2 góc này ở vị trí đồng vị
=> BD//EC

BD là phân giác ABC nên ABD = CBD

Có: ABD + CBD + BEC = 180^o

=> 2.CBD + BEC = 180^o (1)

Tam giác BEC có: BE = BC (gt) nên tam giác BEC cân tại B

=> BEC = BCE ( tính chất tam giác cân)

Tam giác BEC có: BEC + BCE + CEB = 180^o ( tổng 3 góc của tam giác)

=> 2.BCE + CEB = 180^o (2)

Từ (1) và (2) => CBD = BCE

Mà CBD và BCE là 2 góc ở vị trí so le trong nên BD // EC (đpcm)

*Tự vẽ hình

- Xét tam giác BEC có BE=BC(GT)

=> Tam giác BEC cân tại B

=> \(\widehat{E}=\widehat{BCE}\)

- Lại có :\(\widehat{BEC}+\widehat{BCE}=\widehat{ABC}\) (t/c góc ngoài của tam giác)

Mà : \(\widehat{ABD=}\widehat{DBC}=\widehat{\frac{ABC}{2}}\left(GT\right)\)

\(\widehat{ABD}+\widehat{DBC}=\widehat{ABC}\)

\(\widehat{E}=\widehat{BCE};\widehat{E}+\widehat{BCE}=\widehat{ABD}\left(cmt\right)\)

=> \(\widehat{DBC}=\widehat{BCE}\)

Mà chúng là 2 góc so le trong

=> BD//EC