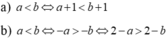Cho A=333444 và B=444333. Hãy so sánh A và B

Những câu hỏi liên quan
bài 1 so sánh
a, 36 và 63
b,4100 và 2200
c, 333444 và 444333
a, 36=3.3.3.3.3.3=729
63=6.6.6=216
729>216 nên 36>63
b, 2200=22.100=(22)100=4100
4100=4100 nên 4100=2200
c, 333444=3334.111=(3334)111
444333=4443.111=(4443)111
Cả hai số đều cùng có số mũ 111 nên ta so sánh 3334 và 4443
3334=(3.111)4=34.1114=81.1114
4443=(4.111)3=43.1113=64.1113
81.1114>64.1113 nên 333444>444333
Đúng 1
Bình luận (0)
a, 36 = (32)3 = 93 > 63 vậy 36 > 63
Các câu khác làm như Lộc
Đúng 0
Bình luận (0)
\(a,3^6=\left(3^2\right)^3=9^3\\ \)
Vì \(9^3>6^3=>3^6>6^3\)
\(b,4^{100}=\left(2^2\right)^{100}=2^{200}\)
Vì \(2^{200}=2^{200}=>4^{100}=2^{200}\)
\(c,333^{444}=111^{444}\cdot3^{444}\\ 444^{333}=111^{333}\cdot4^{333}\\ 3^{444}=\left(3^4\right)^{111}=81^{111}\\4^{333}=\left(4^3\right)^{111}=63^{111} \)
Vì \(111^{444}>111^{333};81^{111}>63^{111}=>333^{444}>444^{333}\)
Đúng 0
Bình luận (0)
cho mình hỏi so sánh các số sau , số nào lớn hơn :
1030 và 2 100 B, 333444 và 444333
\(a.10^{30}=\left(10^3\right)^{10}=1000^{10}\\ 2^{100}=\left(2^{10}\right)^{10}=1024^{10}\)
Vì 100010 < 102410 => 1030 < 2100
\(b,333^{444}=\left(111\cdot3\right)^{444}=111^{444}\cdot3^{444}=111^{444}\cdot81^{111}\\ 444^{333}=\left(111\cdot4\right)^{333}=111^{333}\cdot4^{333}=111^{333}\cdot64^{111}\)
Vì 111444 >111333 ; 81111 > 64111 => 333444 > 444333
Đúng 4
Bình luận (0)
So sánh:
333444 và 444333
333444 và 444333
Ta có: 333444 = 111444 x 3444
444333 = 111333 x 4333
Tách: 3444 = (34)111 =81111 <=>4333 = (43)111 = 64111
Mà: {111444 > 111333 (1)
{81111 > 64111 hay: (34)111 > (43)111 (2)
Từ (1) và (2) ta có:333444 > 444333
Đúng 3
Bình luận (0)
333444 = (3334)111 = ( 34.1114)111 = (81.1114)111
444333 = (4443)111 = (43.1113)111 = (64.1113)111
=> 333444> 444333
333444 và 444333
Ta có: 333444 = 111444 x 3444
444333 = 111333 x 4333
Tách: 3444 = (34)111 =81111 <=>4333 = (43)111 = 64111
Mà: {111444 > 111333 (1)
{81111 > 64111 hay: (34)111 > (43)111 (2)
Từ (1) và (2) ta có:333444 > 44433
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
So sánh.a,
10
30
và
2
100
b,
333
444
và
444
333
c,
21
5
và
27
5
.
49...
Đọc tiếp
So sánh.
a, 10 30 và 2 100
b, 333 444 và 444 333
c, 21 5 và 27 5 . 49 8
d, 3 2 n và 2 3 n n ∈ N *
e, 2017.2019 và 2018 2
f, 100 - 99 2000 và 100 + 99 0
g, 2009 10 + 2009 9 và 2010 10
a, Ta có 10 30 = 10 3 10 = 1000 10
2 100 = 2 10 10 = 1024 10
Vì 1000<1024 nên 1000 10 < 1024 10
Vậy 10 30 < 2 100
b, Ta có: 333 444 = 333 4 111 = 3 . 111 4 111 = 81 . 111 4 111
444 333 = 444 3 111 = 4 . 111 3 111 = 64 . 111 3 111
Vì 81 > 64 và 111 4 > 111 3 nên 81 . 111 4 111 > 64 . 111 3 111
Vậy 333 444 > 444 333
c, Ta có: 21 5 = 3 . 7 15 = 3 15 . 7 15
27 5 . 49 8 = 3 3 5 . 7 2 8 = 3 15 . 7 16
Vì 7 15 < 7 16 nên 3 15 . 7 15 < 3 15 . 7 16
Vậy 21 5 < 27 5 . 49 8
d, Ta có: 3 2 n = 3 2 n = 9 n
2 3 n = 2 3 n = 8 n
Vì 8 < 9 nên 8 n < 9 n n ∈ N *
Vậy 3 2 n > 2 3 n
e, Ta có: 2017.2018 = (2018–1).(2018+1) = 2018.2018+2018.1–1.2018–1.1
= 2018 2 - 1
Vì 2018 2 - 1 < 2018 2 nên 2017.2018< 2018 2
f, Ta có: 100 - 99 2000 = 1 2000 = 1
100 + 99 0 = 199 0 = 1
Vậy 100 - 99 2000 = 100 + 99 0
g, Ta có: 2009 10 + 2009 9 = 2009 9 . 2009 + 1
= 2010 . 2009 9
2010 10 = 2010 . 2010 9
Vì 2009 9 < 2010 9 nên 2010 . 2009 9 < 2010 . 2010 9
Vậy 2009 10 + 2009 9 < 2010 10
Đúng 0
Bình luận (0)
Cho a < b, hãy so sánh: 2a và 2b; 2a và a + b; -a + b; -a và -b.
+ a < b ⇒ 2a < 2b (nhân cả hai vế với 2 > 0, BĐT không đổi chiều).
+ a < b ⇒ a + a < b + a (Cộng cả hai vế với a)
hay 2a < a + b.
+ a < b ⇒ (-1).a > (-1).b (Nhân cả hai vế với -1 < 0, BĐT đổi chiều).
hay –a > -b.
Đúng 0
Bình luận (0)
cho a<b hãy so sánh;
2a và 2b 2a và a+b -a và -b
\(a< b\)
\(\Leftrightarrow2a< 2b\)
\(a< b\)
\(\Leftrightarrow a+a< b+a\)
\(\Leftrightarrow2a< a+b\)
\(a< b\)
\(\Leftrightarrow-1a>-1b\)
\(\Leftrightarrow-a>-b\)
Đúng 0
Bình luận (0)
Do \(a< b\) , nên :
Gọi \(a=2,b=3\)
+ \(2a\Leftrightarrow2.2=4\)
\(2b=2.3=6\)
Mà \(4< 6\) \(\Rightarrow2a< 2b\)
+ \(2a\Leftrightarrow2.2=4\)
\(a+b\Leftrightarrow2+3=5\)
Mà \(4< 5\) \(\Rightarrow2a< a+b\)
+ \(-a\Leftrightarrow-1.2=-2\)
\(-b\Leftrightarrow-1.3=-3\)
Mà \(-2>-3\) \(\Rightarrow-a>-b\)
Đúng 1
Bình luận (0)
Cho a > b, hãy so sánh
a) a + b và 2b; b) 1- a và 1 - b.
Cho a < b, hãy so sánh:
a) a + 1 và b + 1; b) 2 - a và 2 - b
a, Cho a,b,n ϵ N* . Hãy so sánh dfrac{a+n}{b+n}vàdfrac{a}{b}b, Cho A dfrac{10^{11}-1}{10^{12}-1};Bdfrac{10^{10}+1}{10^{11}+1}. So sánh A và B
Đọc tiếp
a, Cho a,b,n ϵ N* . Hãy so sánh \(\dfrac{a+n}{b+n}và\dfrac{a}{b}\)
b, Cho A= \(\dfrac{10^{11}-1}{10^{12}-1};B=\dfrac{10^{10}+1}{10^{11}+1}.\) So sánh A và B
Lời giải:
a) Xét hiệu \(\frac{a+n}{b+n}-\frac{a}{b}=\frac{(a+n).b-a(b+n)}{b(b+n)}=\frac{n(b-a)}{b(b+n)}\)
Nếu $b>a$ thì $\frac{a+n}{b+n}-\frac{a}{b}>0\Rightarrow \frac{a+n}{b+n}>\frac{a}{b}$
Nếu $b<a$ thì $\frac{a+n}{b+n}-\frac{a}{b}<0\Rightarrow \frac{a+n}{b+n}<\frac{a}{b}$
Nếu $b=a$ thì $\frac{a+n}{b+n}-\frac{a}{b}=0\Rightarrow \frac{a+n}{b+n}=\frac{a}{b}$
b) Rõ ràng $10^{11}-1< 10^{12}-1$.
Đặt $10^{11}-1=a; 10^{12}-1=b; 11=n$ thì: $a< b$; $A=\frac{a}{b}$ và $B=\frac{10^{11}+10}{10^{12}+10}=\frac{a+n}{b+n}$
Áp dụng kết quả phần a:
$b>a\Rightarrow \frac{a+n}{b+n}>\frac{a}{b}$ hay $B>A$
Đúng 2
Bình luận (2)
Cho A = a5c6 + 4b7d và B = abcd + 4576.Hãy so sánh A và B
\(A=1000a+500+10c+6+4000+100b+70+d\)
\(=1000a+100b+10c+d+4576\)
=B
Đúng 1
Bình luận (0)