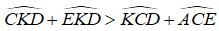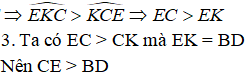Cho ΔABC có AB < AC. Vẽ đường cao BE và CD. Chứng minh: BD > CE.

Những câu hỏi liên quan
cho ΔABC ⊥ A, có BC=5cm,AC=3cm. Trên tia đối của tia CB đặt đoạn thẳng CD=6cm. Qua D kẻ đường thẳng vuông góc với BD, cắt AC tại E
A) chứng minh: ΔABC∼ΔDEC
b) Vẽ AH⊥BC(H thuộc BC) và DK⊥ CE(K thuộc CE). chứng minh rằng CH. CD=CK.CA
lưu ý: nhớ kèm theo hình vẽ và bài giải
a: Xét ΔBAC vuông tại A và ΔBDE vuông tại D có
góc B chung
=>ΔBAC đồng dạng với ΔBDE
b: Xét ΔCHA vuông tại H và ΔCKD vuông tại K có
góc HCA=góc KCD
=>ΔCHA đồng dạngvơi ΔCKD
=>CH/CK=CA/CD
=>CH*CD=CK*CA
Đúng 0
Bình luận (1)
Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H.a) Chứng minh rằng : ΔABE ∽ ΔACF. Từ đó suy ra AF. AB = AE. AC b) Chứng minh rằng : ΔAEF ∽ ΔABC. c) Vẽ DM vuông góc AC tại M. Gọi K là giao điểm của CH và DM . Chứng minh rằng CD/BD=CM/EMvà BH/EH=DK/MKd) Chứng minh rằng AH. AD + CH. CF = CD^4 / CM^2
a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
\(\widehat{BAE}\) chung
Do đó: ΔABE\(\sim\)ΔACF
Suy ra: \(\dfrac{AB}{AC}=\dfrac{AE}{AF}\)
hay \(AF\cdot AB=AE\cdot AC\)
b: Ta có: \(\dfrac{AB}{AC}=\dfrac{AE}{AF}\)
nên \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
\(\widehat{FAE}\) chung
Do đó: ΔAEF\(\sim\)ΔABC
Đúng 0
Bình luận (3)
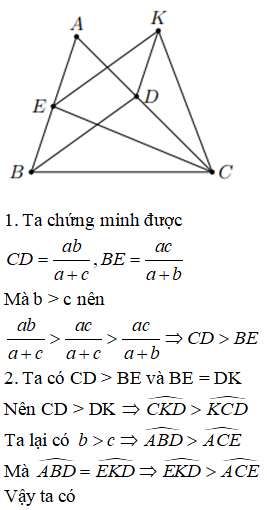
Bài 23/ Cho tam giác ABC có BC = a, AC = b, AB = c (b > c), các đường phân giác BD,
CE.
a) Tính các độ dài CD, BE rồi suy ra CD > BE
b) Vẽ hình bình hành BEKD. Chứng minh CE > EK
c) Chứng minh CE > BD.
1. Cho ΔABC. Trên nửa mặt phẳng bờ AB không chứa điểm B vẽ AD ⊥ và bằng AB; Trên nửa mặt phẳng bờ AC không chứa điểm C vẽ AE ⊥ và bằng AC.a) Chứng minh CD BE và CD ⊥ BEb) Gọi M là trung điểm của BC. Chứng minh AM 1/2 DE và AM ⊥ DE2. Cho ΔABC qua A vẽ một đường thẳng xy // BC. Từ điểm M trên cạnh BC vẽ các đường thẳng // AB và AC chúng cắt xy theo thứ tự tại D và E. Cmr:a) ΔABC ΔMDEb) Ba đường thẳng AM, DB, CE cùng đi qua một điểm( đồng qui)3. ΔABC vuông cân tại A, có cạnh AB 1cm. Vẽ AH ⊥ BC...
Đọc tiếp
1. Cho ΔABC. Trên nửa mặt phẳng bờ AB không chứa điểm B vẽ AD ⊥ và bằng AB; Trên nửa mặt phẳng bờ AC không chứa điểm C vẽ AE ⊥ và bằng AC.
a) Chứng minh CD = BE và CD ⊥ BE
b) Gọi M là trung điểm của BC. Chứng minh AM = 1/2 DE và AM ⊥ DE
2. Cho ΔABC qua A vẽ một đường thẳng xy // BC. Từ điểm M trên cạnh BC vẽ các đường thẳng // AB và AC chúng cắt xy theo thứ tự tại D và E. Cmr:
a) ΔABC = ΔMDE
b) Ba đường thẳng AM, DB, CE cùng đi qua một điểm( đồng qui)
3. ΔABC vuông cân tại A, có cạnh AB = 1cm. Vẽ AH ⊥ BC (H ∈ BC).
a) Chứng minh ΔABH = ΔACH
b) Tính AH
c) M là một điểm di chuyển trên cạnh BC, kẻ MP, MQ lần lượt ⊥ AB và AC. Chứng minh MP + MQ không đổi.
Cho ΔABC cân tại A, đường cao AH. Biết AB = AC = 17cm, AH = 15cm.
a) Tính BH và BC.
b) Từ B kẻ BD ⊥ AC (D ∈ AC). Chứng minh: ΔAHC ∼ ΔBDC.
c) Qua D vẽ DE ⊥ bc (E ∈ BC). Chứng minh: BE.EC = \(\dfrac{AH^2.CE^2}{CH^2}\).
c) \(\widehat{BDE}=90^0-\widehat{CDE}=\widehat{BCE}\)
\(\Rightarrow\)△BDE∼△DCE (g-g) \(\Rightarrow\dfrac{BE}{DE}=\dfrac{DE}{CE}\Rightarrow BE.CE=DE^2\left(1\right)\)
-△AHC có: AH//DE (cùng vuông góc BC) \(\Rightarrow\dfrac{DE}{AH}=\dfrac{CE}{CH}\Rightarrow DE=\dfrac{CE.AH}{CH}\Rightarrow DE^2=\dfrac{AH^2.CE^2}{CH^2}\left(2\right)\)
-Từ (1) và (2) ta có điều cần phải c/m.
Đúng 2
Bình luận (0)
Cho tam giâc ABC có đường cao AH.Lấy điểm k sao cho AK =BC .Vẽ BD vuông góc và bằng AB(D,C thuộc 2 nử mf đối nhau bờ AB)
Vẽ CE vuông góc và bằng AC (E, B thuộc 2 nử mf đối nhau bờ AC)
Chứng minh AH, BE, CD đồng quy
Cho ΔABC nhọn (AB<AC). Từ B, C vẽ đường cao BD, CE.
a) Chứng minh: ΔABD đồng dạng với ΔAEC
b) Chứng minh: góc ABC + góc EDC = 180 độ
c) M, N lần lượt là trung điểm của BD, CE. Vẽ AK ( K∈BC) là tia phân giác góc MAN. Chứng minh: KB.AC = KC.AB
Cho ΔABC cân tại A (Å < 90 độ). Vẽ BE vuông góc với AC tại E, CD vuông góc với AB tại D.
a/ Chứng minh BE = CD
b/ Cho BC = 10cm, BD = 6cm. Tính CD
c/ Chứng minh AD = AE
d/ Gọi I là giao điểm của BE và CD. Chứng minh ΔBIC cân
e/ Chứng minh AI là tia phân giáp của góc BAC
a: Xét ΔABE vuông tại E và ΔACD vuông tại D có
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACD
b: \(CD=\sqrt{10^2-6^2}=8\left(cm\right)\)
c: Ta có: ΔABE=ΔACD
nên AE=AD
d: Xét ΔDBC vuông tại D và ΔECB vuông tại E có
BC chung
DC=BE
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{IBC}=\widehat{ICB}\)
hay ΔBIC cân tại I
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A có AH là đường cao, biết AB = 15cm, AC=20cm, BC = 25cm. Gọi E là trung điểm của AH, trên tia BA lấy điểm D sao cho điểm A là trung điểm của BD. DH cắt AC và CE lần lượt tại I và K. Chứng minh: DI.DK + CI.CA = CD2.