Làm giúp em câu C

Những câu hỏi liên quan
mọi người giúp em câu b và câu c với ạ, câu (a) em làm được rồi.
Đọc tiếp
mọi người giúp em câu b và câu c với ạ, câu (a) em làm được rồi.
Giúp em bài 4 câu c,d với ah (Những câu trên em làm đc rồi)
Làm cho em bài 3 với ạ , làm giúp em câu C thôi ạ.Em cảm ơn ạ 
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM⊥AB
Đúng 0
Bình luận (0)
Làm giúp em bài 1 câu (c) và câu (d) với ạ 
Làm giúp em câu c thui ạ
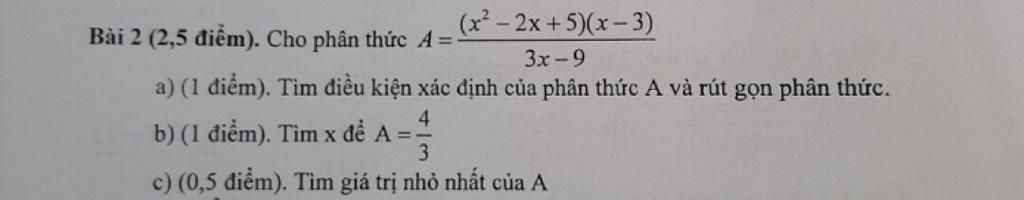
a: \(A=\dfrac{\left(x^2-2x+5\right)\left(x-3\right)}{3\left(x-3\right)}=\dfrac{x^2-2x+5}{3}\)
Đúng 1
Bình luận (0)
Làm giúp em câu C thôi ạ
a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKC vuông tại K có KF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AK^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AK là đường cao ứng với cạnh huyền BC, ta được:
\(KB\cdot KC=AK^2\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(AF\cdot AC=KB\cdot KC\)
b: Xét tứ giác AFKE có
\(\widehat{AFK}=\widehat{AEK}=\widehat{EAF}=90^0\)
Do đó: AFKE là hình chữ nhật
Suy ra: \(AK=FE\left(3\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKB vuông tại K có KE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AK^2\left(4\right)\)
Từ \(\left(3\right),\left(4\right)\) suy ra \(AE\cdot AB=FE^2\)
c: Ta có: \(AF\cdot AC+AE\cdot AB+KB\cdot KC\)
\(=AK^2+AK^2+AK^2\)
\(=3\cdot AK^2=3\cdot FE^2\)
Đúng 0
Bình luận (0)

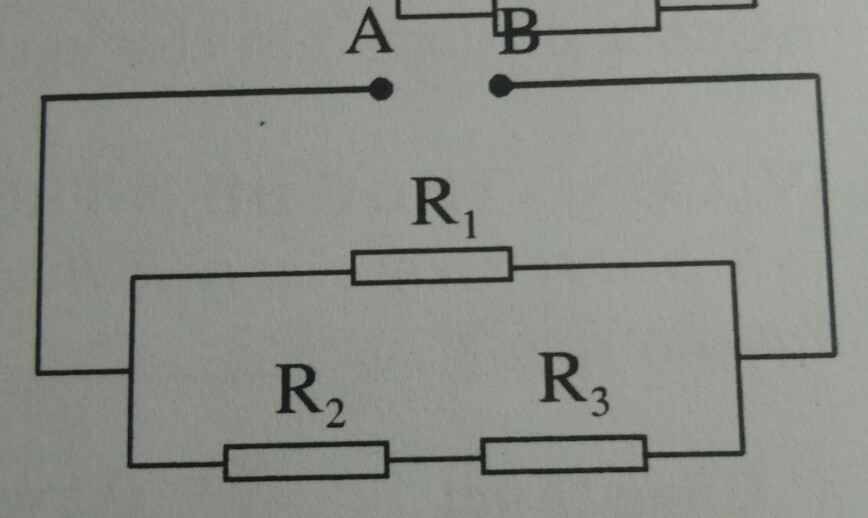
Làm giúp em câu C thôi ạ
\(a.R_{tđ}=\dfrac{R_1.\left(R_2+R_3\right)}{R_1+R_2+R_3}=\dfrac{6.\left(2+4\right)}{6+2+4}=3\Omega\\ b.U_{AB}=I.R_{tđ}=2.3=6V\\ c.Vì.R_1//R_{23}\Rightarrow U_{AB}=U_1=U_{23}=6V\\ I_1=\dfrac{U_1}{R_1}=\dfrac{6}{6}=1A\\ I_{23}=I-I_1=2-1=1A\\ Vì.R_2ntR_3\Rightarrow I_{23}=I_2=I_3=1A\)
Đúng 4
Bình luận (0)
Làm giúp em câu c với ạ
c: Thay x=2y vào (P), ta được:
y=2*(2y)^2
=>8y^2-y=0
=>y=0 hoặc y=1/8
=>x=0 hoặc 2x^2=1/8
=>\(x\in\left\{0;\dfrac{1}{4};-\dfrac{1}{4}\right\}\)
Đúng 0
Bình luận (0)
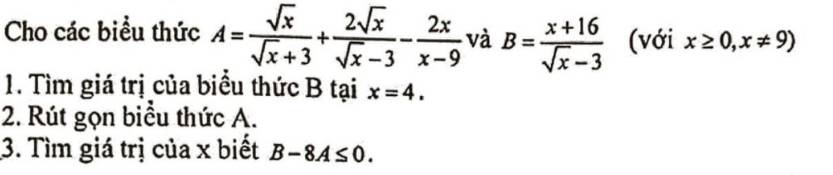
Làm giúp em câu c vs ạ
Rút gọn được \(A=\dfrac{\sqrt{x}}{\sqrt{x}-3}\)
\(B-8A\le0\Leftrightarrow\dfrac{x+16}{\sqrt{x}-3}-\dfrac{8\sqrt{x}}{\sqrt{x}-3}\le0\)
\(\Leftrightarrow\dfrac{x-8\sqrt{x}+16}{\sqrt{x}-3}\le0\)
\(\Leftrightarrow\dfrac{\left(\sqrt{x}-4\right)^2}{\sqrt{x}-3}\le0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}-4=0\\\sqrt{x}-3< 0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=16\\x< 9\end{matrix}\right.\)
Kết hợp ĐKXD ta được: \(\left[{}\begin{matrix}x=16\\0\le x< 9\end{matrix}\right.\)
Đúng 1
Bình luận (0)




















