a, Chứng minh được  B A C ^ = 90 0  kết hợp  B A D ^ = C A E ^ = 90 0 => ĐPCM

b, Chứng minh ∆BAD:∆EAC => AD.AE=AB.AC(đpcm)

c, Chứng minh tứ giác OIO’K là hình chữ nhật

Đường tròn ngoại tiếp ∆OKO’ chính là đường tròn ngoại tiếp hình chữ nhật ,có đường kính là IK mà IK ⊥ BC tại I

a)     Xét (O): AI và DI là 2 tiếp tuyến cắt nhau tại I (gt)

=> AI = DI (TC 2 tiếp tuyến cắt nhau)

CMTT: AI = EI  (TC 2 tiếp tuyến cắt nhau)

=> AI = EI = DI

Mà  DE = EI + DI

=>AI = EI = DI =\(\dfrac{DE}{2}\)

Xét tam giác ADE có: AI = EI = DI =\(\dfrac{DE}{2}\)(cmt)

=> Tam giác ADE vuông tại A (định lý đảo đường trung tuyến trong tam giác vuông)

=> ^MAN = 90^o

Xét tam giác AID: AI = DI (cmt) => Tam giác AID cân tại I 

Mà IM là đường phân giác AID (AI và DI là 2 tiếp tuyến cắt nhau tại I)

=>  IM là đường cao

=> ^IMA = 90^o

CMTT: ^ANI = 90^o

Xét TG AMIN:

 ^IMA = 90^o (cmt)

^ANI = 90^o (cmt)

^MAN = 90^o (cmt)

=> AMIN là hình chữ nhật (dhnb)

b) Xét tam giác OAI vuông tại A, AM là đường cao ( do AM vg góc OI)

=> IM.IO = IA² (HTL) (1)

Xét tam giác O'AI vuông tại A, AN là đường cao ( do AN vg góc O'I)

=> IN.IO' = IA² (HTL) (2)

Từ (1) và (2) => IM.IO = IN.IO’ (đpcm)

c) Xét (O) và (O'): 2 đường tròn (O) và (O’) tiếp xúc ngoài tại A (cmt)

=> A \(\in\)OO' (TC đường nối tâm)

mà IA vg góc AO (do AI là tiếp tuyến trong của 2 đường tròn (O) và (O’) tiếp xúc ngoài tại A )

=> OO' vg góc AI tại A  (*)

Xét tam giác ADE vuông tại A (^DAE = 90^o do AMIN là hcn)

I là TĐ của DE (do ID = IE = \(\dfrac{DE}{2}\))

=> I là tâm đường tròn đường kính DE, nội tiếp tam giác ADE  

=> A \(\in\)(I) (**)

Từ (*) và (**) => OO’ là tiếp tuyến của đường tròn đường kính DE có A là tiếp điểm.

d) Xét tg OIO' vuông tại I, AI là đường cao:

AI² = AO . AO' (HTL)

=> AI²= R. R'

Mà AI = \(\dfrac{DE}{2}\)(cmt)

=> (\(\dfrac{DE}{2}\))² = R . R'

<=> \(\dfrac{DE^2}{4}\) = R . R'

<=> DE = 2\(\sqrt{R.R'}\)

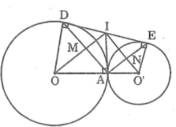
Ta có: IA = ID = IE (chứng minh trên)

Suy ra A nằm trên đường tròn tâm I đường kính DE

Vì OO’ ⊥ IA tại A nên OO’ là tiếp tuyến của đường tròn (I; DE/2)

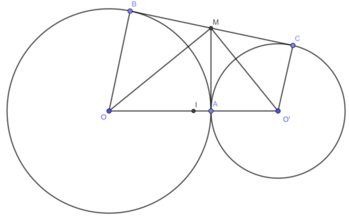
Ta có:

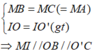
Mà OB ⊥ BC ⇒ IM ⊥ BC

Ta có:

IM ⊥ BC

BC ⋂ (I; IM) = {M}

Suy ra, BC là tiếp tuyến của đường tròn tâm I, bán kính IM