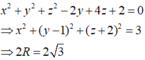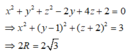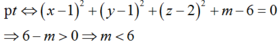giải phương trình: (x2-6x+11)(y2+2y+4) = -z2+4z+2

Những câu hỏi liên quan
Cho mặt cầu (S) có phương trình
x
2
+
y
2
+
z
2
-
6
x
-
2
y
-
4
z
-
5
0
. Gọi A là giao điểm của mặt cầu (S) với tia Oz. Tìm tọa độ của điểm A A. (0;0;5) B. (5;0;0) C. (0;-5;0) D. (0;5;0)
Đọc tiếp
Cho mặt cầu (S) có phương trình x 2 + y 2 + z 2 - 6 x - 2 y - 4 z - 5 = 0 . Gọi A là giao điểm của mặt cầu (S) với tia Oz. Tìm tọa độ của điểm A
A. (0;0;5)
B. (5;0;0)
C. (0;-5;0)
D. (0;5;0)
Tìm độ dài đường kính của mặt cầu (S) có phương trình
x
2
+
y
2
+
z
2
−
2
y
+
4
z
+
2
0.
A.
2
3
B. 2. C. 1. D.
3
Đọc tiếp
Tìm độ dài đường kính của mặt cầu (S) có phương trình x 2 + y 2 + z 2 − 2 y + 4 z + 2 = 0.
A. 2 3
B. 2.
C. 1.
D. 3
Tìm độ dài đường kính của mặt cầu (S) có phương trình
x
2
+
y
2
+
z
2
-2y+4z+2 0
Đọc tiếp
Tìm độ dài đường kính của mặt cầu (S) có
phương trình x 2 + y 2 + z 2 -2y+4z+2 = 0
![]()
![]()
![]()
![]()
Tìm GTNNA x2 + y2 – 6x + 4y + 20B 9x2 + y2 + 2z2 – 18x + 4z – 6y +30C x2 +y2 + z2 – xy – yz – zx + 3D 5x2 + 2y2 + 4xy – 2x + 4y + 2021E x2 – 2x+ 4y2 + 4y + 2014F 5x2 + 5y2 + 8xy + 2y – 2x + 30K x2 + 4y2 + z2 – 2x + 12y – 4z +44Giúp mik vs cần gấp!!!!
Đọc tiếp
Tìm GTNN
A= x2 + y2 – 6x + 4y + 20
B= 9x2 + y2 + 2z2 – 18x + 4z – 6y +30
C= x2 +y2 + z2 – xy – yz – zx + 3
D= 5x2 + 2y2 + 4xy – 2x + 4y + 2021
E= x2 – 2x+ 4y2 + 4y + 2014
F= 5x2 + 5y2 + 8xy + 2y – 2x + 30
K= x2 + 4y2 + z2 – 2x + 12y – 4z +44
Giúp mik vs cần gấp!!!!
$A=x^2+y^2-6x+4y+20=(x^2-6x+9)+(y^2+4y+4)+7$
$=(x-3)^2+(y+2)^2+7\geq 0+0+7=7$
Vậy $A_{\min}=7$. Giá trị này đạt tại $(x-3)^2=(y+2)^2=0$
$\Leftrightarrow x=3; y=-2$
---------------------
$B=9x^2+y^2+2z^2-18x+4z-6y+30$
$=(9x^2-18x+9)+(y^2-6y+9)+(2z^2+4z+2)+10$
$=9(x^2-2x+1)+(y^2-6y+9)+2(z^2+2z+1)+10$
$=9(x-1)^2+(y-3)^2+2(z+1)^2+10\geq 10$
Vậy $B_{\min}=10$. Giá trị này đạt tại $(x-1)^2=(y-3)^2=(z+1)^2$
$\Leftrightarrow x=1; y=3; z=-1$
Đúng 1
Bình luận (0)
$C=x^2+y^2+z^2-xy-yz-xz+3$
$2C=2x^2+2y^2+2z^2-2xy-2yz-2xz+6$
$=(x^2-2xy+y^2)+(y^2-2yz+z^2)+(x^2-2xz+z^2)+6$
$=(x-y)^2+(y-z)^2+(z-x)^2+6\geq 6$
$\Rightarrow C\geq 3$
Vậy $C_{\min}=3$. Giá trị này đạt tại $x-y=y-z=z-x=0$
$\Leftrihgtarrow x=y=z$
--------------------------------------
$D=5x^2+2y^2+4xy-2x+4y+2021$
$=2(y^2+2xy+x^2)+3x^2-2x+4y+2021$
$=2(x+y)^2+4(x+y)+3x^2-6x+2021$
$=2(x+y)^2+4(x+y)+2+3(x^2-2x+1)+2016$
$=2[(x+y)^2+2(x+y)+1]+3(x^2-2x+1)+2016$
$=2(x+y+1)^2+3(x-1)^2+2016\geq 2016$
Vậy $D_{\min}=2016$ khi $x+y+1=x-1=0$
$\Leftrightarrow x=1; y=-2$
Đúng 1
Bình luận (0)
$E=x^2-2x+4y^2+4y+2014$
$=(x^2-2x+1)+(4y^2+4y+1)+2012$
$=(x-1)^2+(2y+1)^2+2012$
$\geq 2012$
Vậy $E_{\min}=2012$. Giá trị này đạt tại $x-1=2y+1=0$
$\Leftrightarrow x=1; y=\frac{-1}{2}$
----------------------
$F=5x^2+5y^2+8xy+2y-2x+30$
$=4(x^2+2xy+y^2)+x^2+y^2+2y-2x+30$
$=4(x+y)^2+(x^2-2x+1)+(y^2+2y+1)+28$
$=4(x+y)^2+(x-1)^2+(y+1)^2+28\geq 28$
Vậy $F_{\min}=28$. Giá trị này đạt tại $x+y=x-1=y+1=0$
$\Leftrightarrow x=1; y=-1$
Đúng 1
Bình luận (0)
1) Tìm x, y, z
a) 9x2 +y2 + 2z2 – 18x +4z – 6y +20 = 0
b) 5x2 +5y2 +8xy+2y – 2x+2 = 0
c) 5x2 +2y2 + 4xy – 2x + 4y +5 = 0
d) x2 + 4y2 + z2 =2x + 12y – 4z – 14
e) x2 +y2 – 6x + 4y +2= 0
Giúp mik vs cần gấp!!!
\(a,\Leftrightarrow\left(9x^2-18x+9\right)+\left(y^2-6y+9\right)+\left(2z^2+4z+2\right)=0\\ \Leftrightarrow9\left(x-1\right)^2+\left(y-3\right)^2+2\left(z+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\\z=-1\end{matrix}\right.\)
\(b,\Leftrightarrow\left(4x^2+8xy+4y^2\right)+\left(x^2-2x+1\right)+\left(y^2+2y+1\right)=0\\ \Leftrightarrow4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=-y\\x=1\\y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(c,\Leftrightarrow\left(4x^2+4xy+y^2\right)+\left(x^2-2x+1\right)+\left(y^2+4y+4\right)=0\\ \Leftrightarrow\left(2x+y\right)^2+\left(x-1\right)^2+\left(y+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}2x=-y\\x=1\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Đúng 4
Bình luận (0)
a,9x^2+y^2+2z^2−18x+4z−6y+20=0
⇔9(x−1)^2+(y−3)^2+2(z+1)^2=0
⇔x=1;y=3;z=−1
b,5x^2+5y^2+8xy+2y−2x+2=0
⇔4(x+y)2+(x−1)2+(y+1)2=0
⇔x=−y;x=1y=−1⇔x=1y=−1
c,5x^2+2y^2+4xy−2x+4y+5=0
⇔(2x+y)^2+(x−1)^2+(y+2)^2=0
⇔2x=−y;x=1;y=−2
⇔x=1;y=−2
⇔(x−1)^2+(2y−3)^2+(z+2)^2=0
Đúng 2
Bình luận (0)
\(d,\Leftrightarrow\left(x^2-2x+1\right)+\left(4y^2-12y+9\right)+\left(z^2+4z+4\right)=0\\ \Leftrightarrow\left(x-1\right)^2+\left(2y-3\right)^2+\left(z+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{3}{2}\\z=-2\end{matrix}\right.\)
\(e,x^2+y^2-6x+4y+2=0\\ \Leftrightarrow\left(x-3\right)^2+\left(y+2\right)^2=11\)
\(\Rightarrow\)PT vô nghiệm vì 11 không phải là tổng 2 số chính phương
Đúng 2
Bình luận (0)
Cho mặt cầu (S) có phương trình và mặt phẳng (P):
x
2
+
y
2
+
z
2
- 2x - 2y + 4z + 2 0. Mặt cầu (S) và mặt phẳng (P) có giao nhau khi:
Đọc tiếp
Cho mặt cầu (S) có phương trình và mặt phẳng (P): x 2 + y 2 + z 2 - 2x - 2y + 4z + 2 = 0. Mặt cầu (S) và mặt phẳng (P) có giao nhau khi:

![]()
![]()
![]()
Chọn B
Mặt cầu (S) có tâm I(1;1;-2) và bán kính

Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, tìm tất cả các giá trị m để phương trình
x
2
+
y
2
+
z
2
-
2
x
-
2
y
-
4
z
+
m
0
là phương trình của một mặt cầu.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, tìm tất cả các giá trị m để phương trình x 2 + y 2 + z 2 - 2 x - 2 y - 4 z + m = 0 là phương trình của một mặt cầu.
![]()
![]()
![]()
![]()
Trong không gian hệ tọa độ Oxyz, tìm tất cả các giá trị của m để phương trình
x
2
+
y
2
+
z
2
-
2
x
-
2
y
-
4
z
+
m
0
là...
Đọc tiếp
Trong không gian hệ tọa độ Oxyz, tìm tất cả các giá trị của m để phương trình x 2 + y 2 + z 2 - 2 x - 2 y - 4 z + m = 0 là phương trình của một mặt cầu.
A. m ≤ 6
B. m>6
C. m<6
D. m ≥ 6
Chọn C
Phương trình x 2 + y 2 + z 2 - 2 x - 2 y - 4 z + m = 0 là một phương trình mặt cầu
![]()
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt cầu (S) có phương trình:
x
2
+
y
2
+
z
2
- 2x - 2y - 4z + 5 0Trong các khẳng định sau, khẳng định nào sai? A. Mặt cầu (S) có tâm I(1;1;2) và đường kính có độ dài bằng 2. B. Phương trình chính tắc của mặt cầu (S) là:
(
x
...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình: x 2 + y 2 + z 2 - 2x - 2y - 4z + 5 = 0
Trong các khẳng định sau, khẳng định nào sai?
A. Mặt cầu (S) có tâm I(1;1;2) và đường kính có độ dài bằng 2.
B. Phương trình chính tắc của mặt cầu (S) là: ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 2 ) 2 = 1
C. Diện tích của mặt cầu (S) là π
D. Thể tích của khối cầu (S) là 4π/3
Đáp án A
Ta viết lại phương trình của (S) dưới dạng chính tắc như sau:
x 2 + y 2 + z 2 - 2x - 2y - 4z + 5 = 0
<=> ( x 2 - 2x + 1) +( y 2 - 2y + 1) + ( z 2 - 4z + 4) = 1 + 1 + 4 - 5
<=> ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 2 ) 2 = 1
Vậy khẳng định B đúng.
Mặt cầu (S) có tâm I(1;1;2) và có bán kính R=1, do đó đường kính của (S) là 2R=2.
Vậy khẳng định A đúng.
Thể tích của khối cầu (S) là 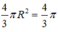 .
.
Vậy khẳng định D đúng.
Đúng 0
Bình luận (0)
Cho mặt cầu (S) có phương trình
x
2
+
y
2
+
z
2
-
2
x
-
2
y
+
4
z
+
2
0
và mặt phẳng
P
:
2
x
-
3
y
+
z
-
m
0
. Mặt cầu (S) và mặt phẳng (P) có giao nhau khi: A. ...
Đọc tiếp
Cho mặt cầu (S) có phương trình x 2 + y 2 + z 2 - 2 x - 2 y + 4 z + 2 = 0 và mặt phẳng P : 2 x - 3 y + z - m = 0 . Mặt cầu (S) và mặt phẳng (P) có giao nhau khi:
A. m < - 3 - 2 14 h o ặ c m > - 3 + 2 14
B. - 3 - 2 14 ≤ m ≤ - 3 + 2 14
C. - 2 - 3 14 ≤ m ≤ - 2 + 3 14
D. - 2 - 3 14 < m < - 2 + 3 14