Cho P=x3+x2_11x+m và Q=x-2.Tìm m để P chia hết cho Q.

Những câu hỏi liên quan
\(\text{a) Cho P = x3 + 6x2 + 12x + a và Q = x + 2 Hãy tìm a để đa thức P chia hết cho đa thức Q? b) Tìm n \varepsilon ℤ để 2n^2 - n + 2 chia hết cho đa thức Q}\)
cho P = x3+x2-11x+m và Q=x-2. tìm m để P chia hết cho Q
Gọi thương của phép chia \(P\)cho \(Q\)là \(A\)
Ta có: \(P=Q.A\)
\(\Leftrightarrow\)\(x^3+x^2-11x+m=\left(x-2\right).A\)
Vì biểu thức luôn đúng với mọi \(x\)nên ta thay \(x=2\)ta được:
\(8+4-22+m=0\)
\(\Leftrightarrow\)\(m-10=0\)
\(\Leftrightarrow\)\(m=10\)
Vậy...
Đúng 0
Bình luận (0)
To \(P⋮Q\)then \(P=Q.g\left(x\right)\)
<=> P = ( x - 2 ) . g(x)
replace x = 2 to P we have
\(2^3+2^2-11.2+m=8+4-22+m=0\)
\(-12+m=0\)
=> \(m=12\)
Thus , m=12
Đúng 0
Bình luận (0)
Cho đa thức: f(x)= 3x4+9x3+7x+2 và g(x)=x+3
a) Thực hiện phép chia f(x) : g(x)
b) Tìm số nguyên âm x để f(x) chia hết cho g(x)
c) tìm m để đa thức k(x)= -x3-5x+2m chia hết cho g(x)
\(a,f\left(x\right):g\left(x\right)=\left(3x^4+9x^3+7x+2\right):\left(x+3\right)\\ =\left[3x^3\left(x+3\right)+7\left(x+3\right)-19\right]:\left(x+3\right)\\ =\left[\left(3x^3+7\right)\left(x+3\right)-19\right]:\left(x+3\right)\\ =3x^3+7.dư.19\)
\(c,\) Để \(k\left(x\right)⋮g\left(x\right)\Leftrightarrow-x^3-5x+2m=\left(x+3\right)\cdot a\left(x\right)\)
Thay \(x=-3\)
\(\Leftrightarrow-\left(-3\right)^3-5\left(-3\right)+2m=0\\ \Leftrightarrow27+15+2m=0\\ \Leftrightarrow2m=-42\\ \Leftrightarrow m=-21\)
Đúng 1
Bình luận (0)
Cho p(x)=x4+x3+62-40x+m-1985, trong đó m là một tham số
a) tìm m để p(x) chia hết cho (x-2)
b) với m mới vừa tìm được, giải phương trình P(x)=0
a: P(x) chia hết cho x-2
=>x^4-2x^3+3x^3-6x^2+12x^2-24x-16x+32+m-2017 chia hết cho x-2
=>m-2017=0
=>m=2017
b: P(x)=x^4+x^3+6x^2-40x+32
P(x)=0
=>x^4-2x^3+3x^3-6x^2+12x^2-24x-16x+32=0
=>(x-2)(x^3+3x^2+12x-16)=0
=>x^3+3x^2+12x-16=0 hoặc x-2=0
=>x^3-x^2+4x^2-4x+16x-16=0 hoặc x-2=0
=>x-1=0 hoặc x=2
=>x=1 hoặc x=2
Đúng 0
Bình luận (0)
Tìm giá trị của m để đa thức x 3 + 3 x 2 - 5 x + m chia hết cho ( x - 2 )
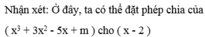
để tìm số dư, rồi cho số dư đó bằng 0, từ đó tìm được giá trị của m.
Mở rộng: Bài toán này ta áp dụng phân tích đa thức thành nhân tử để giải toán

Đúng 0
Bình luận (0)
Tìm m để đa thức A ( x ) = x 3 – 3 x 2 + 5 x + m chia hết cho đa thức B ( x ) = x – 2
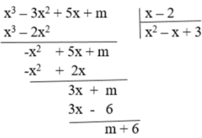
A(x) chia hết cho B(x) khi m + 6 = 0 ⇒ m= -6
Đúng 0
Bình luận (0)
Cho đa thức p(x)= 48x4 - 28x3 - 24x2 + mx +1 và q(x)= 2x2 + nx -1. Tìm m và n để p(x) chia hết cho q(x)
1.Tìm x:
a)2x(x+1)-2x2=4
b)x3-16x=0
c)(3x+1)2-8x2+2x=-6
2.Tìm m để đa thức f(x)=x3+6x2+12x+m chia hết cho đa thức h(x)=x+2
Bài 2:
x^3+6x^2+12x+m chia hết cho x+2
=>x^3+2x^2+4x^2+8x+4x+8+m-8 chia hết cho x+2
=>m-8=0
=>m=8
Đúng 0
Bình luận (0)
cho đa thức P(x)= 48x^4 - 28x^3 - 24X^2 + mx + 1 và Q(x)= 2x^2 +nx-1
A) tìm m,n để đa thức P(x) chia hết cho Q(x)
B) với m vừa tìm được ở a, hãy tìm các nghiệm của P(x)
a) Tìm a để đa thức x3+x2-x+a chia hết cho đa thức x+2
b) Tìm a và b để đa thức x3+ax2+2x+b chia hết cho đa thức x2+x+1
c) Tìm a và b để đa thức x3+4x2+ax+b chia hết cho đa thức x2+x+1
em mong mọi người giúp đỡ em cảm ơn ạ

















