Cho hàm số y = 2x+3
a) Vẽ đồ thị hàm số trên
b) Gọi A,B là giao điểm của đồ thị với các trục tọa độ . Tính diện tích tam giác OAB ( O là góc tọa độ và đơn vị trên các trục tọa độ là cm )
c ) Tính góc tạo bởi đường thẳng y=ax+b và trục Ox
Cho hàm số y= -2x+3
a) Vẽ đồ thị của hàm số trên
b) Gọi A và B là giao điểm của đồ thị với các trục tọa độ. Tính diện tích tam giác OAB (với O là gốc tọa độ và đơn vị trên các trục tọa độ là centimet)
c) Tính góc tạo bởi đường thẳng y= -2x+3 với trục Ox
Cho đồ thị hàm số y = x + 4
b) Gọi A, B lần lượt là giao điểm của đồ thị hàm số với các trục Ox, Oy. Tính diện tích tam giác OAB ( đơn vị đo trên trục tọa độ là cm)
b) Ta có:
S A O B = 1/2 OA.OB = 1/2 |-4|.4 = 8 ( c m 2 )
cho hàm số y= -1/2x+3
a. Vẽ đồ thị hàm số trên
b. gọi A,B là giao điểm của đồ thị hàm số với các trục tọa độ. Tính diện tích OAB (bới O là gốc tọa độ)
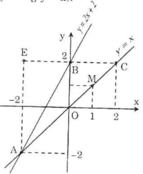
a) Vẽ đồ thị của các hàm số y = x và y = 2x + 2 trên cùng một mặt phẳng tọa độ.
b) Gọi A là giao điểm của hai đồ thị nói trên, tìm tọa độ điểm A.
c) Vẽ qua điểm B(0; 2) một đường thẳng song song với trục Ox, cắt đường thẳng y = x tại điểm C. Tìm tọa độ điểm C rồi tính diện tích tam giác ABC (đơn vị đo trên các trục tọa độ là xentimet)
a) Vẽ đường thẳng qua O(0; 0) và điểm M(1; 1) được đồ thị hàm số y = x.
Vẽ đường thẳng qua B(0; 2) và A(-2; -2) được đồ thị hàm số y = 2x + 2.
b) Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình:
2x + 2 = x
=> x = -2 => y = -2
Suy ra tọa độ giao điểm là A(-2; -2).
c) Qua B(0; 2) vẽ đường thẳng song song với Ox, đường thẳng này có phương trình y = 2 và cắt đường thẳng y = x tại C.
- Tọa độ điểm C:
Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình:
x = 2 => y = 2 => tọa độ C(2; 2)
- Tính diện tích tam giác ABC: (với BC là đáy, AE là chiều cao tương ứng với đáy BC)
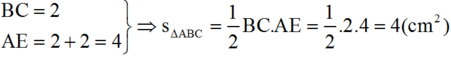
a)
+) y = 2x + 2
Cho x = 0 => y = 2
=> ( 0 ; 2 )
y = 0 => x = -1
=> ( -1 ; 0 )
- Đồ thị hàm số y = x đi qua 2 điểm có tọa độ ( 0 ; 0 )
- Đồ thị hàm số y = 2x + 2 đi qua 2 điểm có tọa độ ( 0 ; 2 ) và ( -1 ; 0 )
b) Hoành độ điểm A là nghiệm của PT sau :
x = 2x + 2
<=> 2x - x = -2
<=> x = -2
=> y = -2
Vậy A ( -2 ; -2 )
c) Tung độ điểm C = 2 => hoành độ điểm C là x = 2
=> C ( 2 ; 2 )
Từ A hạ \(AH\perp BC\), ta có : AH = 4cm
BC = 2cm
Vậy : ..............
\(\Rightarrow S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}.4.2=4\left(cm^2\right)\)
Cho hàm số y = 2x và y = -3x + 5
a) Vẽ trên cùng một hệ trục tọa độ, đồ thị hai hàm số trên?
b) Tìm tọa độ giao điểm M của hai đồ thị bằng phương pháp đại số. Gọi A, B lần lượt là giao điểm của đường thẳng y = -3x + 5 với trục hoành và trục tung. Tính diện tích tam giác OAB và diện tích tam giác OMA.
Cho hàm số y= x+2
A) vẽ đồ thị hàm số
B) gọi AB là giao điểm của đồ thị với 2 trục tọa độ xác định toạ độ của điểm A,B và tính diện tích của tam giác AOB ( đơn vị đo trên các trục tọa độ là xen-ti-mét vuông )
Cho các hàm số y= 2x2 có đồ thị là (P) và y = 2x + 4 có đồ thị là (d).
a) Vẽ P và d trên cùng một hệ trục tọa độ vuông góc (đơn vị trên các trục bằng nhau) (Làm rồi)
b) xác định tọa độ giao điểm của P và d bằng phép tính. ( Làm rồi)
c) Gọi A,B là hai giao điểm (P) và (d), tính diện tích tam giác AOB. (Chưa làm được)
Từ Phương trình hoành độ giao điểm sẽ tìm được tọa độ của A ( x1,y1) và B (x2 , y2)
Bạn Vẽ hình . Gọi M là hình chiếu của A trên Ox , N là Hình chiếu của B trên Ox . tiếp theo bạn tính lần lượt các diện tích sau.:
1. S tam giác AMO vuông tại M
2. S tam giác BNO vuông tại N
3. S Hình Thang AMNB .
=> S tam giác AOB = S Hình thang AMNB - ( S tam giác AMO + S tam giác BNO)
Cho hai hàm số y = 4x + 2 (1)và hàm số y = 2x - 2(2)câu a vẽ đồ thị câu b tìm tọa độ giao điểm m của hai hàm số trên câu c tìm tọa độ a b là giao điểm của hai đồ thị hàm số 1 2 với trục ox câu d tính chu vi diện tích tam giác MAB + e tính các góc của tam giác MAB
a:
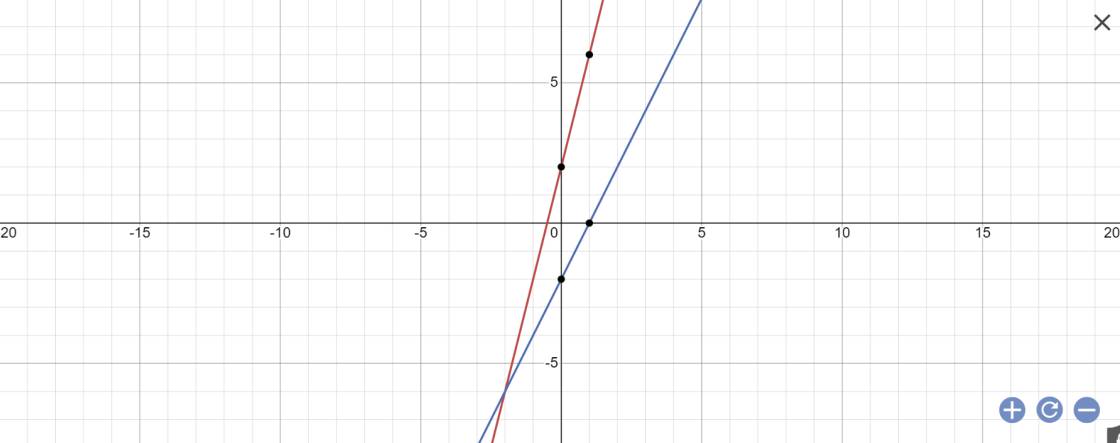
b: phương trình hoành độ giao điểm là:
4x+2=2x-2
=>4x-2x=-2-2
=>2x=-4
=>x=-2
Thay x=-2 vào y=4x+2, ta được:
\(y=4\cdot\left(-2\right)+2=-8+2=-6\)
Vậy: M(-2;-6)
c: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\4x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\4x=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-\dfrac{1}{2}\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\2x-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\2x=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=1\end{matrix}\right.\)
Vậy: B(1;0); A(-1/2;0)
d: M(-2;-6); B(1;0); A(-1/2;0)
\(MA=\sqrt{\left(-\dfrac{1}{2}+2\right)^2+\left(0-6\right)^2}=\dfrac{3\sqrt{17}}{2}\)
\(MB=\sqrt{\left(1+2\right)^2+\left(0+6\right)^2}=3\sqrt{5}\)
\(AB=\sqrt{\left(-\dfrac{1}{2}-1\right)^2+\left(0-0\right)^2}=\dfrac{3}{2}\)
Chu vi tam giác MAB là:
\(C_{MAB}=MA+MB+AB=\dfrac{3}{2}+3\sqrt{5}+\dfrac{3\sqrt{17}}{2}\)
Xét ΔMAB có \(cosAMB=\dfrac{MA^2+MB^2-AB^2}{2\cdot MA\cdot MB}=\dfrac{9}{\sqrt{85}}\)
=>\(sinAMB=\sqrt{1-\left(\dfrac{9}{\sqrt{85}}\right)^2}=\dfrac{2}{\sqrt{85}}\)
Diện tích tam giác MAB là:
\(S_{AMB}=\dfrac{1}{2}\cdot MA\cdot MB\cdot sinAMB=\dfrac{1}{2}\cdot\dfrac{3\sqrt{17}}{2}\cdot3\sqrt{5}\cdot\dfrac{2}{\sqrt{85}}\)
\(=\dfrac{9}{2}\)
a:
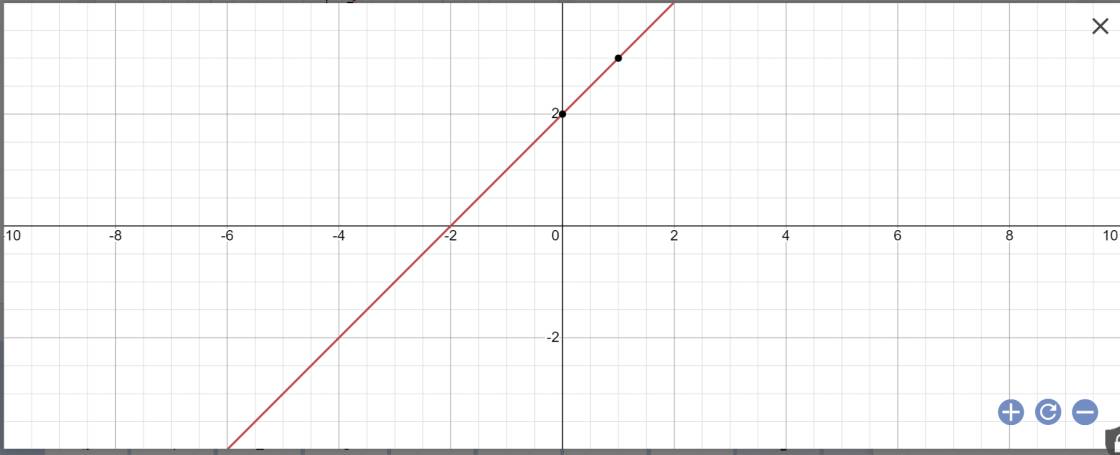
b:
Sửa đề: Tính diện tích tam giác ABO
tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\x+2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.\)
Vậy: A(-2;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0+2=2\end{matrix}\right.\)
Vậy: B(0;2)
O(0;0) A(-2;0); B(0;2)
\(OA=\sqrt{\left(-2-0\right)^2+\left(0-0\right)^2}=\sqrt{4}=2\)
\(OB=\sqrt{\left(0-0\right)^2+\left(2-0\right)^2}=\sqrt{4}=2\)
\(AB=\sqrt{\left(0+2\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)
Vì \(OA^2+OB^2=AB^2\)
nên ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot2\cdot2=2\)
c: Sửa đề: Tính góc tạo bởi đường thẳng với trục ox
Gọi \(\alpha\) là góc tạo bởi đường thẳng y=x+2 với trục Ox
\(tan\alpha=a=1\)
=>\(\alpha=45^0\)