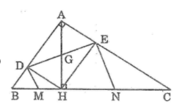
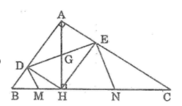
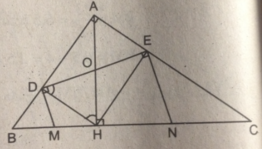
Cho tam giác ABC vuông tại A đường cao ah chia cạnh huyền bc thành hai đoạn bh=4cm và ch=9cm gọi dvaf elầmn lượt là hình chiếu của h trên ab và ac
A giải tam giác abc
b tínhđộ dài de
C các đường thẳng vuông góc với de tại d và e lần lượt cắt bc tại m và n chứng minh m là trung điểm của bh và n là trung điểm của của ch
Dtinhs diện tích tứ giác demn