Question

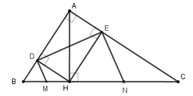
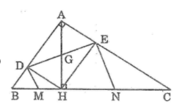
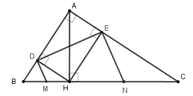
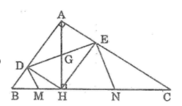
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền BC thành hai đoạn BH, CH có độ dài lần lượt là 4cm, 9cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC. Các đường thẳng vuông góc với DE tại D và tại E lần lượt cắt BC tại M và N. Chứng minh M là trung điểm của BH và N là trung điểm của CH

Answer 1

*Gọi G là giao điểm của AH và DE

Ta có: GA = GD = GH = GE (tính chất hình chữ nhật)

Suy ra tam giác GHD cân tại G

Suy ra tam giác NCE cân tại N ⇒ NC = NE     (16)

Từ (13) và (16) suy ra: NC = NH hay N là trung điểm của CH.