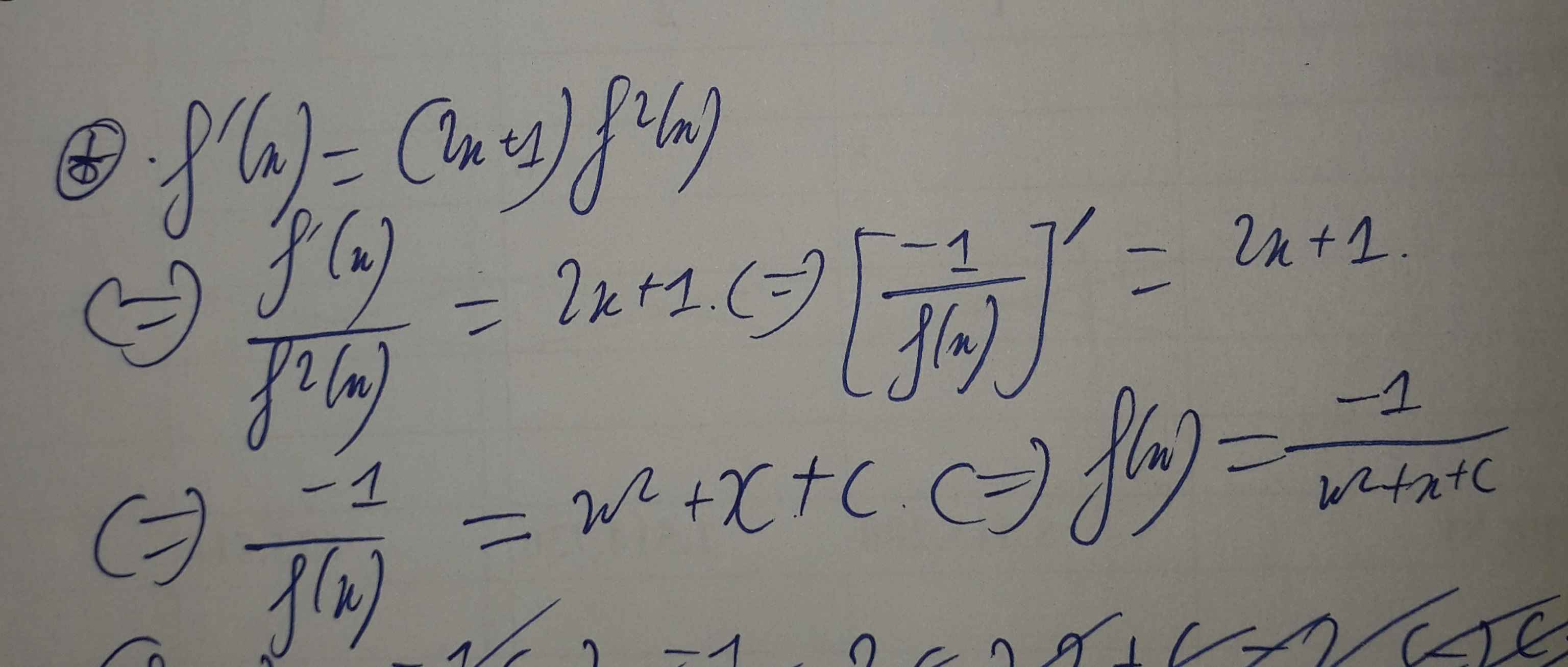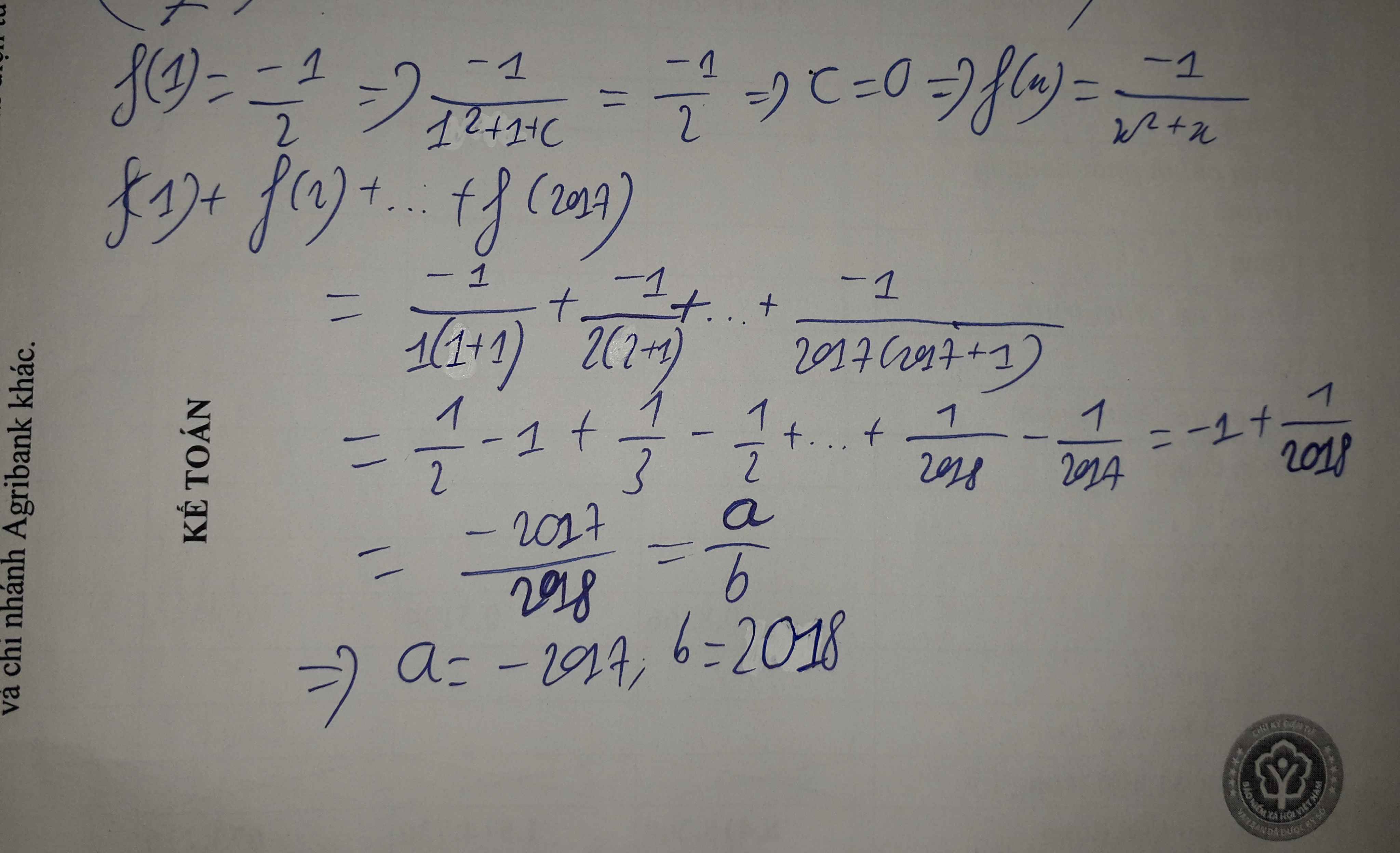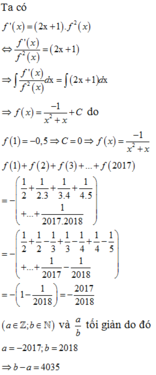Cho hàm số y=f(x)=2017^2x/2017^2x+2017. Tính f(a)+f(b)biết a+b=1

Những câu hỏi liên quan
Cho hàm số y = f(x) = ax4 + bx2 + c biết a > 0, c > 2017 và a + b + c < 2017. Số cực trị của hàm số y = |f(x) – 2017| là
A. 1
B. 3
C. 7
D. 5
cho hàm số y = f(x) xác định và f(x) \(\ne0\) \(\forall x\in\left(0;+\infty\right)\), \(f'\left(x\right)=\left(2x+1\right)f^2\left(x\right)\) và f(1) = -1/2. Biết tổng f(1) + f(2) + f(3) + ... + f(2017) = a/b (a,b\(\in R\)) với a/b tối giản. Tìm a,b
Cho hàm số
f
(
x
)
a
x
4
+
b
x
2
+
c
v
ớ
i
a
0
,
c
2017
,
a
+
b
+
c
2017
.
Số cực trị của hàm...
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 2 + c v ớ i a > 0 , c > 2017 , a + b + c < 2017 . Số cực trị của hàm số y = | f ( x ) - 2017 | là
A. 1
B. 5
C. 3
D. 7
Đáp án D
Phương pháp:
+) Xét hàm số h(x) = f(x) - 2017 = ax4 + bx2 + c - 2017
+) Tìm số điểm cực trị của hàm số h(x) bằng cách giải phương trình h'(x) = 0
+) Xác định dấu của h(0); h(1); h(-1) và vẽ đồ thị hàm số y = h(x), từ đó vẽ đồ thị hàm số y = |h(x)| và kết luận.
Cách giải:
Xét hàm số h(x) = f(x) - 2017 = ax4 + bx2 + c - 2017,
với a > 0, c > 2017, a + b + c < 2017 nên b < 0
![]()
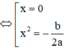
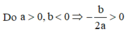
![]()
Ta có: h(0) = c - 2017 > 0, h(-1) = h(1) = a + b + c - 2017 < 0
⇒ h(0).(h-1) < 0, h(0).h(1) < 0
⇒ ∃ x1, x2: x1 ∈ (-1;0), x2 ∈ (0;1) mà h(x1) = h(x2) = 0
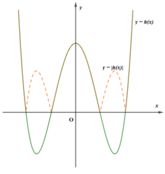
Do đó, đồ thị hàm số y = h(x) và y = |h(x)| dạng như hình vẽ bên.
Vậy, số cực trị của hàm số y = |f(x) - 2017| là 7
Đúng 0
Bình luận (0)
Biết hàm số
F
(
x
)
-
x
1
-
2
x
+
2017
là một nguyên hàm của hàm số
f
x
a
x
+
b
1
-
2
x
. Khi đó tổng của a và b là A. 3. B. 2. C. 0. D...
Đọc tiếp
Biết hàm số F ( x ) = - x 1 - 2 x + 2017 là một nguyên hàm của hàm số f x = a x + b 1 - 2 x . Khi đó tổng của a và b là
A. 3.
B. 2.
C. 0.
D. 1.
Chọn B.
Ta có F ' ( x ) = - x 1 - 2 x + 2017 ' = 3 x - 1 1 - 2 x
Nên a = 3; b = -1
=> a + b = 3 + (-1) = 2
Đúng 0
Bình luận (0)
Cho hàm số \(y=f\left(x\right)=\dfrac{2017^{2x}}{2017^{2x}+2017}\)
Tính \(f\left(a\right)+f\left(b\right)\) biết \(a+b=1\)
(đăng lại hộ cho thằng bạn Phạm Quốc Cường cho dễ nhìn)
\(y=f\left(x\right)\dfrac{2017^{2x}}{2017^{2x}+2017}\)
\(\Rightarrow\left\{{}\begin{matrix}f\left(a\right)=\dfrac{2017^{2a}}{2017^{2a}+2017}\\f\left(b\right)=\dfrac{2017^{2b}}{2017^{2b}+2017}\end{matrix}\right.\)
\(\Rightarrow f\left(a\right)+f\left(b\right)=\dfrac{2017^{2a}}{2017^{2a}+2017}+\dfrac{2017^{2b}}{2017^{2b}+2017}\)
\(=\dfrac{2017^{2a}\left(2017^{2b}+2017\right)}{\left(2017^{2a}+2017\right)\left(2017^{2b}+2017\right)}+\dfrac{2017^{2b}\left(2017^{2a}+2017\right)}{\left(2017^{2a}+2017\right)\left(2017^{2b}+2017\right)}\)
\(=\dfrac{2017^{2\left(a+b\right)}+2017^{2a+1}+2017^{2\left(a+b\right)}+2017^{2b+1}}{2017^{2\left(a+b\right)}+2017^{2a+1}+2017^{2b+1}+2017^2}\)
\(=\dfrac{2017^{2\left(a+b\right)}+2017^{2a+1}+2017^{2\left(a+b\right)}+2017^{2b+1}}{2017^{2\left(a+b\right)}+2017^{2a+1}+2017^{2\left(a+b\right)}+2017^{2b+1}}=1\) (Vì a+b=1)
P/S:Nhìn chữ \(f\left(a\right)\) thấy khổ cho số phận mềnh quá :((
Đúng 0
Bình luận (4)
Bao giờ xong thì tag Phạm Quốc Cường lên xem lời giải nhé em
Đúng 0
Bình luận (0)
Cho hàm số f(x) liên tục trên R và f(x) ≠ 0 với mọi
x
∈
R
. f (x) (2x+1)f2(x) và f(1) –0,5. Biết rằng tổng f(1) + f(2) + f(3) + ... + f(2017)
a
b
; (a
∈
Z, b
∈
N) với
a
b
tối giản. Mệnh đề nào dưới đây đúng? A.
a
∈...
Đọc tiếp
Cho hàm số f(x) liên tục trên R và f(x) ≠ 0 với mọi x ∈ R . f '(x) = (2x+1)f2(x) và f(1) = –0,5. Biết rằng tổng f(1) + f(2) + f(3) + ... + f(2017) = a b ; (a ∈ Z, b ∈ N) với a b tối giản. Mệnh đề nào dưới đây đúng?
A. a ∈ - 2017 ; 2017
B. b - a = 4035
C. a + b = - 1
D. a b < - 1
Đáp án B.
Phương pháp : Chuyển vế, lấy nguyên hàm hai vế.
Cách giải :
![]()
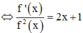
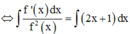
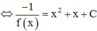
![]()
![]()
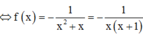
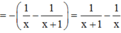
![]()
![]()
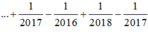
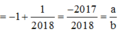
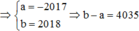
Đúng 0
Bình luận (0)
Cho hàm số yf(x) xác định trên R và có
f
(
x
)
(
x
-
1
)
2017
(
x
2
-
1
)
(
2
x
+
3
)
3
. Hàm số yf(x) có bao nhiêu điểm cực trị? A. 1 B. 4 C. 3 D. 2
Đọc tiếp
Cho hàm số y=f(x) xác định trên R và có f ' ( x ) = ( x - 1 ) 2017 ( x 2 - 1 ) ( 2 x + 3 ) 3 . Hàm số y=f(x) có bao nhiêu điểm cực trị?
A. 1
B. 4
C. 3
D. 2
Đáp án D
f ' ( x ) = 0 ⇔ ( x - 1 ) 2017 ( x 2 - 1 ) ( 2 x + 3 ) 3 = 0 ⇔ x = 1 x = - 1 x = - 3 2
Xét dấu:
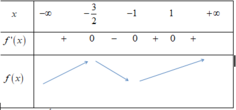
Vậy hàm số có 2 cực trị
Đúng 0
Bình luận (0)
cho hàm số f(x)=a^2x+b(a,b thuộc Z,a khác 0) a)so sánh f(2015/2016) và f(2016/2017).b)chứng minh không thể đồng thời có f(17)=1+2+2^2+...+2^80 và f(10)=1
Cho hàm số
f
(
x
)
liên tục trên
ℝ
và
f
(
x
)
≠
0
với mọi
x
∈
ℝ
thỏa mãn
f
(
x
)
(
2
x
+
1
)
.
f
2
(
x...
Đọc tiếp
Cho hàm số f ( x ) liên tục trên ℝ và f ( x ) ≠ 0 với mọi x ∈ ℝ thỏa mãn f ' ( x ) = ( 2 x + 1 ) . f 2 ( x ) v à f ( 1 ) = - 0 , 5 . Biết tổng f ( 1 ) + f ( 2 ) + f ( 3 ) + . . . + f ( 2017 ) = a b ; ( a ∈ ℝ ; b ∈ ℝ ) v ớ i a b tối giản. Mệnh đề nào dưới đây đúng?
A. b - a = 4035
B. a + b = - 1
C. a b < - 1
D. a ∈ - 2017 ; 2017