Tam giác nhọn ABC có đường cao BD, CE, tia phâm giác của góc ABD cắt CE và CA theo thứ tự tại K và N, tia phân giác cúa góc ACE cắt BD và BA theo thứ tự tại I và M. MNIK là hình gì? Vì sao?

Những câu hỏi liên quan
Tam giác nhọn ABC có đường cao BD, CE, tia phâm giác của góc ABD cắt CE và CA theo thứ tự tại K và N, tia phân giác cúa góc ACE cắt BD và BA theo thứ tự tại I và M. MNIK là hình gì? Vì sao?
Cho tam giác ABC nhọn , đường cao BD và CE . Tia phân giác của góc ABD cẳ CE , CA theo thứ tự tại K và N , tia phân giác của góc ACE cắt BD và BA tại I và M . Chứng minh :
a) góc ABD = góc ACE
b) O là giao điểm của CM và BN biết góc BOC = 90 độ
c) MNIK là hình thoi
Bài 17. Cho tam giác ABC cân tại A (góc A nhọn), các đường cao BD, CE cắt nhau
tại H. Tia phân giác của góc ABD cắt CE và AC theo thứ tự tại M và P. Tia
phân giác của góc ACE cắt BD và AB theo thứ tự ở Q và N. BP cắt CN tại O.
Chứng minh
1. góc ABD = góc ACE (*)
2. BH = CH. (*)
3. Tam giác BOC là tam giác vuông cân.
4. MNP Q là hình vuông.
(*) GẤP Ạ 2 CÂU ĐÓ CŨNG OKK
1: ΔABD vuông tại D
=>\(\widehat{ABD}+\widehat{BAD}=90^0\)
=>\(\widehat{ABD}+\widehat{BAC}=90^0\left(1\right)\)
ΔACE vuông tại E
=>\(\widehat{ACE}+\widehat{CAE}=90^0\)
=>\(\widehat{ACE}+\widehat{BAC}=90^0\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{ABD}=\widehat{ACE}\)(3)
2: \(\widehat{ABD}+\widehat{DBC}=\widehat{ABC}\)
\(\widehat{ACE}+\widehat{ECB}=\widehat{ACB}\)
mà \(\widehat{ABD}=\widehat{ACE};\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{DBC}=\widehat{ECB}\)
=>\(\widehat{HBC}=\widehat{HCB}\)
=>ΔHBC cân tại H
=>HB=HC
3: BO là phân giác của góc ABD
=>\(\widehat{ABO}=\dfrac{1}{2}\cdot\widehat{ABD}\left(4\right)\)
CO là phân giác của góc ACE
=>\(\widehat{ACO}=\dfrac{1}{2}\cdot\widehat{ACE}\left(5\right)\)
Từ (3),(4),(5) suy ra \(\widehat{ABO}=\widehat{ACO}\)
\(\widehat{ABO}+\widehat{OBC}=\widehat{ABC}\)
\(\widehat{ACO}+\widehat{OCB}=\widehat{ACB}\)
mà \(\widehat{ABO}=\widehat{ACO};\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{OBC}=\widehat{OCB}\)
=>OB=OC
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC các đường cao BD, CE. Tia phân giác của góc ABD cắt AC và AB theo thứ tự tại N và M, tia BN cắt CE tại K. Tia CM cắt BD tại H. Chứng minh BN vuông góc với CM
Cho tam giác ABC cân tại A, các đường cao BD,CE cắt nhau tại H. Tia phân giác của góc ABD cắt EC, AC theo thứ tự ở M và P. Tia phân giác góc ACE cắt DB, PB và AB theo thứ tự ở Q, O, N.
Chứng minh rằng :
a ) Góc ABD = góc ACE.
b ) BH = CH.
c ) Tam giác BOC vuông cân.
d ) MNPQ là hình vuông
Cho tam giác ABC nhọn có 2 đường cao BD và CE. Tia phân giác của các góc ABD và ACE cắt nhau tại O và lần lượt cắt AC, AB tại N,M. Tia BN cắt CE tại K, tai CM cắt BD tại H. Chứng minh:
a) BN vuông góc với CM.
b) Tứ giác MNHK là hình thoi
cíu iêm với ;-;
Cho tam giác ABC nhọn, các đường cao BD, CE. Tia phân giác của các góc
A
B
D
^
v
à
A
C
E
^
cắt nhau tại O, và lần lượt cắt AC, AB tại N, M. Tia BN cắt CE tại K, tia CM cắt BD tại H: Chứng minh rằng:a) BN ^ CM;b) Tứ giác MNFIK là hình thoi
Đọc tiếp
Cho tam giác ABC nhọn, các đường cao BD, CE. Tia phân giác của các góc A B D ^ v à A C E ^ cắt nhau tại O, và lần lượt cắt AC, AB tại N, M. Tia BN cắt CE tại K, tia CM cắt BD tại H: Chứng minh rằng:
a) BN ^ CM;
b) Tứ giác MNFIK là hình thoi
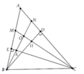
a) Sử dụng tính chất tổng các góc trong một tam giác bằng 1800.
⇒ A B C ^ = A E C ^ ⇒ N B D ^ = M C A ^
Trong DDBN có: N B D ^ + B N D ^ = 90 0
Gọi O = CM Ç BN Þ CM ^ BN = O (1)
b) Xét DCNK có: CO ^ KN Þ CO ^ BN, CO là phân giác A C E ^ nên DCNK cân ở C Þ O là trung điểm KN (2).
Tương tự chứng minh được là trung điểm MH (3).
Từ (1),(2) và (3) suy ra MNHK là hình thoi.
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, các đường cao BD,CE. Tia phân giác của các góc ABD và ACE cắt nhau tại O, cắt AC và AB lần lượt tại N,M. Tia BN cắt CE tại K, tia CM cắt BD tại H. Chứng minh rằng.
a) BN vuông góc với CM.
b) tứ giác MNHK là hình thoi.
cho tam giác nhọn ABC , đường cao BD , CE , tia phân giác của các góc ABD và ACE cắt nhau tại O , cắt AC và AB lần lượt tại N và M . tia BN cắt CE tại K , tia CM cắt BD tại H . Chứng minh :
a, BN vuông góc CM
b, MNHK là hình thoi













