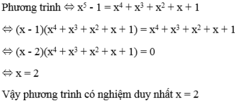Tính trung bình cộng các nghiệm của phương trình : x5=x4+x3+x2+x+2

Những câu hỏi liên quan
Gọi x1, x2 là nghiệm của phương trình x^2+2009x+1=0,
x3,x4 là nghiệm của phương trình x^2+2010x+1=0.
Tính giá trị biểu thức (x1+x3)(x2+x3)(x1-x4)(x2-x4)
Giải phương trình: x 5 = x 4 + x 3 + x 2 + x + 2
Giải các phương trình sau:a, (9x2 - 4)(x + 1) (3x +2)(x2 - 1)b, (x - 1)2 - 1 + x2 (1 - x)(x + 3)c, (x2 - 1)(x + 2)(x - 3) (x - 1)(x2 - 4)(x + 5)d, x4 + x3 + x + 1 0e, x3 - 7x + 6 0f, x4 - 4x3 + 12x - 9 0g, x5- 5x3 + 4x 0h, x4 - 4x3 + 3x2 + 4x - 4 0
Đọc tiếp
Giải các phương trình sau:
a, (9x2 - 4)(x + 1) = (3x +2)(x2 - 1)
b, (x - 1)2 - 1 + x2 = (1 - x)(x + 3)
c, (x2 - 1)(x + 2)(x - 3) = (x - 1)(x2 - 4)(x + 5)
d, x4 + x3 + x + 1 = 0
e, x3 - 7x + 6 = 0
f, x4 - 4x3 + 12x - 9 = 0
g, x5- 5x3 + 4x = 0
h, x4 - 4x3 + 3x2 + 4x - 4 = 0
a, \(\Leftrightarrow\left(9x^2-4\right)\left(x+1\right)-\left(3x+2\right)\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(\left(9x^2-4\right)-\left(\left(3x+2\right)\left(x-1\right)\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-\left(3x^2-x-2\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-3x^2+x+2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x^2+x-2\right)=0\)
\(\Leftrightarrow\left(x+1\right)=0;3x^2+x-2=0\)
=> x=-1
với \(3x^2+x-2=0\)
ta sử dụng công thức bậc 2 suy ra : \(x=\dfrac{2}{3};x=-1\)
Vậy ghiệm của pt trên \(S\in\left\{-1;\dfrac{2}{3}\right\}\)
Đúng 0
Bình luận (0)
b: \(\Leftrightarrow x^2-2x+1-1+x^2=x+3-x^2-3x\)
\(\Leftrightarrow2x^2-2x=-x^2-2x+3\)
\(\Leftrightarrow3x^2=3\)
hay \(x\in\left\{1;-1\right\}\)
c: \(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x+2\right)\left(x-3\right)-\left(x-1\right)\left(x-2\right)\left(x+2\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left[\left(x+1\right)\left(x-3\right)-\left(x-2\right)\left(x+5\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2-2x-3-x^2-3x+10\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(-5x+7\right)=0\)
hay \(x\in\left\{1;-2;\dfrac{7}{5}\right\}\)
Đúng 0
Bình luận (0)
Giả sử x1, x2 là hai nghiệm của phương trình: x2 – x + A = 0 và x3, x4 là hai nghiệm của phương trình: x2 – 4x + B = 0. Tính A, B biết rằng x1, x2, x3, x4 lập thành một cấp số nhân tăng?
Cho hai phương trình x2+2022x+1=0 (1) và x2+2023x+1 (2).Gọi x1,x2 là nghiệm của phương trình (1) ; x3,x4 là nghiệm của phương trình (2).Giá trị của biểu thức P=(x1+x3)(x2+x3)(x1-x4)(x2-x4) là
A.4045 B.-1 C.1 D.0
Bài 1 : Cho a,b,c là các số hữu tỉ khác 0 sao cho a+b-c/c=a-b+c/b=(-a)+b+c/a
Tính giá trị của biểu thức A=(a+b).(b+c).(c+a)/abc
(LƯU Ý : DẤU / LÀ ...TRÊN.....)
Bài 2 : Cho x,x2,x3,x4,x5,x6 thỏa mãn :
(x2)^2=x1.x3
(x3)^2=x2.x4
(x4)^2=x3.x5
(x5)^2=x4.x6
Chứng minh rằng : x1/x6=(x1+x2+x3+x4+x5/x2+x3+x4+x5+x6)^5
Giusp mk vs nhé các bn !!!
Giả sử đa thức
P
(
x
)
x
5
-
a
x
4
+
b
có năm nghiệm
x
1
;
x
2
;
x
3
;
x
4
;
x
5
Đặt
f
(
x
)...
Đọc tiếp
Giả sử đa thức P ( x ) = x 5 - a x 4 + b có năm nghiệm x 1 ; x 2 ; x 3 ; x 4 ; x 5 Đặt f ( x ) = x 2 - 4 Tìm giá trị nhỏ nhất của P = f ( x 1 ) f ( x 2 ) f ( x 3 ) f ( x 4 ) f ( x 5 )
A. 512
B. -512
C. 1024
D. -1024
Cho x1 ,x2, x3 , x4 , x5 thuộc z.
Biết x1+x2=x3+x4=x4+x5=2 và
Tất cả 5 số cộng lại = 0
Tính x5 , x4 và x3
giải
ta có :
\(x1+x2+x3+x4+x5=0\)
\(\left(x1+x2\right)+\left(x3+x4\right)+x5=0\)
\(\Rightarrow2+2+x5=0\Rightarrow x5=-4\)
mà \(x4+x5=2\Rightarrow x4+-4=2\Rightarrow x4=6\)
mặt khác : \(x3+x4=2\Rightarrow x3+6=2\Rightarrow x3=-4\)
vậy : x5 = -4 , x4 = 6 , x3 = -4
Ta có : \(\left\{{}\begin{matrix}x_1+x_2=2\left(I\right)\\x_3+x_4=2\left(II\right)\\x_4+x_5=2\left(III\right)\\x_1+x_2+x_3+x_4+x_5=5\left(IV\right)\end{matrix}\right.\)
Thay (I) và (II) vào (IV) ta được : 2+2+x5=5 => x5=1
Thay x5=1 vào (III) ta được: x4=1
Thay x4=1 vào (II) ta được: x3=1
Vậy x3=x4=x5=1
Cho 2 phương trình
X^2+2020x+1=0 (1)
x^2+2021x+1=0 (2)
Gọi x1 và x2 là nghiệm của (1)
x3 và x4 là nghiệm của (2)
Tính P=(x1+x3)(x2-x4)(x2+x3)(x1-x4)
Cảm ơn mọi người nha
cho x1, x2, x3, x4, x5 thuộc tập hợp số nguyên
biết x1 + x2 + x3 + x4 + x5=0 và x1+ x2 = x3+ x4 = x4+ x5=2
tính x3, x4, x5