giai pt 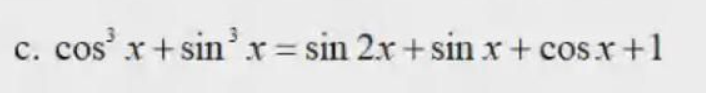

Những câu hỏi liên quan
Giai Pt sau | 4x + 2| - 5x + 3 = 0 nhận được nghiệm?
Giai Pt sau |-4x| = 2 ( x + 1) ta nhận được nghiệm?
Giai Pt sau |x + 2| + x^2 - ( 3 + x) x = 0 ta nhận được nghiệm?
giai giup mik vs
cho pt: 3(a-2)x+2a(x-1)=4a+3 (1)
a) giai pt (1) vs a= -2
b) tim a de pt (1) co nghiem x=1
xin cam on
a) với a = -2 ta được phương trình:
3.[(-2) - 2].x + 2.(-2).(x - 1) = 4.(-2) + 3
<=> 3.(-4x) - 4.(x - 1) = (-8) + 3
<=> -12x - 4(x - 1) = -5
<=> -12x - 4x + 4 = -5
<=> -16x + 4 = -5
<=> -16x = -5 - 4
<=> -16x = -9
<=> x = 9/16
b) để x = 1, ta có:
3.(a - 2).1 + 2a(1 - 1) = 4a + 3
<=> 3(a - 2) + 0 = 4a + 3
<=> 3a - 6 = 4a + 3
<=> 3a - 6 - 4a = 3
<=> -a - 6 = 3
<=> -a = 3 + 6
<=> a = -9
Giai pt
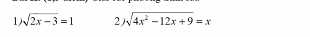
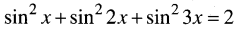
giai pt
ta có sin2(2x)=4sin2xcos2x=4sin2x(1-sin2x)=4sin2x-4sin4x
sin2(3x)=16sin6x-24sin4x+9sin2x=>16sin6x-24sin4x+9sin2x+4sin2x-4sin4x=6
Đặt sin2x=a ta có 16a3-28a2+13a=6
giải tiếp....
Đúng 1
Bình luận (0)
sin2x + sin22x + sin23x = 2
⇔ sin22x = 1 - sin2x + 1 - sin23x
⇔ sin22x = cos2x + cos23x
⇔ \(\dfrac{1-cos4x}{2}=\dfrac{1+cos2x}{2}+\dfrac{1+cos6x}{2}\)
⇔ 1 - cos4x = 2 + cos2x + cos6x
⇔ cos2x + cos6x + cos4x + 1 = 0
⇔ 2cos4x . cos2x + 2cos22x = 0
⇔ \(\left[{}\begin{matrix}cos2x=0\\cos4x+cos2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\2cos3x.cosx=0\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}cos2x=0\\cos3x=0\end{matrix}\right.\). Còn lại tự giải nhé !!
Đúng 0
Bình luận (0)
Giai pt
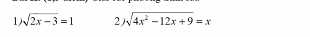
Giai pt 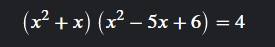
\(\Leftrightarrow x\left(x+1\right)\left(x-2\right)\left(x-3\right)=4\)
\(\Leftrightarrow\left(x^2-2x\right)\left(x^2-2x-3\right)=4\)
Đặt \(x^2-2x=t\)
\(\Rightarrow t\left(t-3\right)=4\)
\(\Leftrightarrow t^2-3t-4=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2-2x=-1\\x^2-2x=4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x+1=0\\x^2-2x-4=0\end{matrix}\right.\) (bấm máy)
Đúng 2
Bình luận (2)
a. Giai pt : 2x(8x-1)^2(4x-2)=9
b. giai pt : x^2-y^2+2x-4y-10=0 vs x,y thuoc so nguyen duong
cho pt: x^2-12x+4=0 c hai nghiem phan biet x1,x2. Khong giai pt, hay tinh gia tri cua bieu thuc: T=x1^2+x2^2/canx1+can x2cho pt: x^2-12x+4=0 c hai nghiem phan biet x1,x2. Khong giai pt, hay tinh gia tri cua bieu thuc: T=x1^2+x2^2/canx1+can x2
Ta có: \(\Delta'=32>0\)
\(\Rightarrow\) Phương trình có 2 nghiệm phân biệt
Theo Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=12\\x_1x_2=4\end{matrix}\right.\)
Mặt khác: \(T=\dfrac{x_1^2+x^2_2}{\sqrt{x_1}+\sqrt{x_2}}\)
\(\Rightarrow T^2=\dfrac{x_1^4+x^4_2+2x_1^2x_2^2}{x_1+x_2+2\sqrt{x_1x_2}}=\dfrac{\left(x_1^2+x_1^2\right)^2}{x_1+x_2+2\sqrt{x_1x_2}}\) \(=\dfrac{\left[\left(x_1+x_2\right)^2-2x_1x_2\right]^2}{x_1+x_2+2\sqrt{x_1x_2}}=\dfrac{\left(12^2-2\cdot4\right)^2}{12+2\sqrt{4}}=1156\)
Mà ta thấy \(T>0\) \(\Rightarrow T=\sqrt{1156}=34\)
Đúng 2
Bình luận (0)
cho pt (a^2-2a-3)*x+a^2=9 giai pt theo a
\(x\left(a^2+a-3a-3\right)+a^2-9=0\)0
\(\Leftrightarrow\left(a-3\right)\left(ax+x+a+3\right)=0\)
nếu \(a=3\)thì phương trình nghiệm đúng với mọi x
nếu \(a\ne3\)thì phương trình có nghiệm a+1
Đúng 0
Bình luận (0)
















