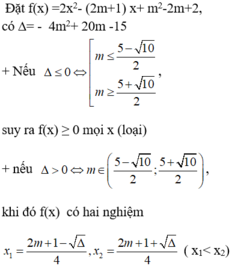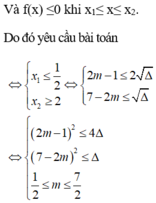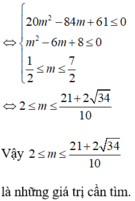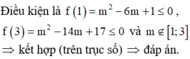Tìm m để (m2 - 2m) chia hết cho 2m+1

Những câu hỏi liên quan
Tìm m thuộc Z để m-1 chia hết cho 2m+1
m-1 chia hết cho 2m+1
2(m-1) chia hết 2m+1
2m-2 chia hết cho 2m+1
2m+1 chia hết cho 2m+1
2m+1-(2m-2) chia hết cho 2m+1
3 chia hết cho 2m +1
Rồi bạn tự làm nha
Đúng 0
Bình luận (0)
Tìm m nguyên để m-1 chia hết cho 2m-1
m-1 chia hết cho 2m-1
2m-1-m chia hết cho 2m-1
=> m chia hết cho 2m-1
=>m-1 và m cùng chia hết cho 2m-1
=>2m-1=1 hoặc 2m-1=-1
=>m=1, m=0
Đúng 0
Bình luận (0)
m-1 chia hết cho 2m-1
=>2(m-1) chia hết cho 2m-1
=>2m-2 chia hết cho 2m-1
=>2m-1-1 chia hết cho 2m-1
Mà 2m-1 chia hết cho 2m-1
=>1 chia hết cho 2m-1
=>\(2m-1\in\left\{-1;1\right\}\)
=>\(2m\in\left\{0;2\right\}\)
=>\(m\in\left\{0;1\right\}\)
Đúng 0
Bình luận (0)
m-1 chia hết cho 2m-1
=>2(m-1) chia hết cho 2m-1
=>2m-2 chia hết cho 2m-1
=>2m-1-1 chia hết cho 2m-1
Mà 2m-1 chia hết cho 2m-1
=>1 chia hết cho 2m-1
=> 2m-1 = {-1;1}
=> 2m = {0;2}
=> m = 0;1
Đúng 0
Bình luận (0)
Cho phương trình
x
2
+ (2m – 1)x +
m
2
– 2m + 2 0. Tìm m để phương trình có hai nghiệm phân biệt cùng dương A.
1
2
m
7
4
B.
m
1
2
C. Cả A và B đúng D. Không có giá trị nào của m
Đọc tiếp
Cho phương trình x 2 + (2m – 1)x + m 2 – 2m + 2 = 0. Tìm m để phương trình có hai nghiệm phân biệt cùng dương
A. 1 2 < m < 7 4
B. m > 1 2
C. Cả A và B đúng
D. Không có giá trị nào của m
Phương trình x 2 + (2m – 1)x + m 2 – 2m + 2 = 0
(a = 1; b = 2m – 1; c = m 2 – 2m + 2)
Ta có ∆ = ( 2 m – 1 ) 2 – 4 . ( m 2 – 2 m + 2 ) = 4 m – 7
Gọi x 1 ; x 2 là hai nghiệm của phương trình, theo hệ thức Vi-ét ta có
Vì a = 1 ≠ 0 nên phương trình có hai nghiệm âm phân biệt ⇔ Δ > 0 P > 0 S > 0
⇔ 4 m − 7 > 0 1 − 2 m > 0 m 2 − 2 m + 2 > 0 ⇔ m > 7 4 m < 1 2 m − 1 2 + 1 > 0 ( l u o n d u n g ) ⇔ m > 7 4 m < 1 2 ( v o l y )
Vậy không có giá trị nào của m thỏa mãn đề bài
Đáp án: D
Đúng 0
Bình luận (0)
Tìm m để 35m3 + 41n2 +13n - 2m để chia hết cho 5x - 2
Tìm m để 35x3 + 41x2 +13x - 2m để chia hết cho 5x - 2
Đặt \(f\left(x\right)=35x^3+41x^2+13x-2m\)
Để \(f\left(x\right)⋮\left(5x-2\right)\Rightarrow f\left(\dfrac{2}{5}\right)=0\)
\(\Rightarrow35.\left(\dfrac{2}{5}\right)^3+41.\left(\dfrac{2}{5}\right)^2+13.\left(\dfrac{2}{5}\right)-2m=0\)
\(\Leftrightarrow14-2m=0\)
\(\Leftrightarrow m=7\)
Đúng 2
Bình luận (4)
Tìm m để bpt 2x2- (2m+1) x+ m2-2m+2≤ 0 nghiệm đúng với mọi
x
∈
1
2
;
2
A.
2
≤
m
≤
21
+
2
34
10
B.
m
≤...
Đọc tiếp
Tìm m để bpt 2x2- (2m+1) x+ m2-2m+2≤ 0 nghiệm đúng với mọi x ∈ 1 2 ; 2
A. 2 ≤ m ≤ 21 + 2 34 10
B. m ≤ 21 + 2 34 10
C. m ≥ 2
D. 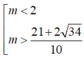
a) Tìm m để hàm số y=(2m-1)x+3 đồng biến .
b) Tìm m để đường thẳng y= ( m2 - 1 )x+2m+1 song song với đường thẳng y=3x+5.
a: Để hàm số đồng biến thì 2m-1>0
hay \(m>\dfrac{1}{2}\)
b: Để hai đồ thị song song thì \(\left\{{}\begin{matrix}m^2-1=3\\2m+1\ne5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\in\left\{2;-2\right\}\\m\ne2\end{matrix}\right.\)
hay m=-2
Đúng 1
Bình luận (0)
Tìm số nguyên m để giá trị của biểu thức m-1 chia hết cho giá trị của biểu thức 2m+1
m - 1 ⋮ 2m - 1
<=> 2(m - 1) ⋮ 2m - 1
<=> 2m - 2 ⋮ 2m - 1
<=> (2m - 1) - 1 ⋮ 2m - 1
=> 1 ⋮ 2m - 1 Hay 2m - 1 là ước của 1
Ư(1) = { ± 1 }
Ta có : 2m - 1 = 1 <=> 2m = 2 => m = 1
2m - 1 = - 1 <=> 2m = 0 => m = 0
Vạy m = { 0; 1 }
Đúng 0
Bình luận (0)
Cho
g
(
x
)
2
x
2
-
4
m
x
+
m
2
-
2
m
-
1...
Đọc tiếp
Cho g ( x ) = 2 x 2 - 4 m x + m 2 - 2 m - 1 x - m 2 . Tìm m để g ( x ) ≤ 0 với ∀ x ∈ 1 ; 3 .
![]()
![]()
![]()
![]()