sắp xếp đa thức theo luỹ thừa giảm dần
(x^3 - 7x + 3 - x^2) : (x- 3)
Thu gọn và sắp xếp đa thức theo lũy thừa giảm dần của biến
cho đa thức A=9-x^3+4x-2x^3+4x^2-6 và B=3+x^3+4x^2+2x^3+7x-6x^3-8x+4
1)thu gọn và sắp xếp đa thức theo lũy thừa giảm dần của biến
2)tìm nghiệm của đa thức A-B
mong mn trả lời giúp ạ
1: \(A\left(x\right)=-3x^3+4x^2+4x+3\)
\(B\left(x\right)=-3x^3+4x^2-x+7\)
2: \(A-B=0\)
=>4x+3-x+7=0
=>3x+10=0
hay x=-10/3
1)
\(A=9-x^3+4x-2x^3+4x^2-6\)
\(A=(9-6)+\left(-x^3-2x^3\right)+4x+4x^2\)
\(A=3-3x^3+4x+4x^2\)
\(A=-3x^3+4x^2+4x+3\)
\(B=3+x^3+4x^2+2x^3+7x-6x^3-8x+4\)
\(B=(3+4)+(x^3+2x^3-6x^3)+4x^2+(7x-8x)\)
\(B=7-3x^3+4x^2-x\)
\(B=-3x^3+4x^2-x+7\)
2) \(A-B=(-3x^3+4x^2+4x+3)-\) \((-3x^3+4x^2-x+7)\)
\(A-B=-3x^3+4x^2+4x+3+\)\(3x^3-4x^2+x-7\)
\(A-B\) \(=\left(-3x^3+3x^3\right)+\left(4x^2-4x^2\right)+\left(4x+x\right)+\left(3-7\right)\)
\(A-B\) \(=5x-4\)
Đặt tên cho đa thức \(5x-4\) là \(H\left(x\right)\)
Cho \(H\left(x\right)=0\)
hay \(5x-4=0\)
\(5x\) \(=0+4\)
\(5x\) \(=4\)
\(x\) \(=4:5\)
\(x\) \(=\) \(0,8\)
Vậy \(x=0,8\) không phải là nghiệm của H(\(x\))
MIK KHÔNG CHẮC LÀ CÂU 2 ĐÚNG
Bài 4: Cho hai đa thức:
P(x)= \(x^5-2x^2+7x^4-9x^3-x+2x^2-5x^4\)
Q(x)= \(5x^4-x^5+4x^2-6+9x^3-8+x^{^{ }5}\)
a) Sắp xếp các hạng tử của mỗi đa thức trên theo luỹ thừa giảm dần của biến
b) Tìm hệ số cao nhất và hệ số tự do của đa thức P(x)
a: \(P\left(x\right)=x^5+2x^4-9x^3-x\)
\(Q\left(x\right)=5x^4+9x^3+4x^2-14\)
b: Hệ số cao nhất của P(x) là 1
Hệ số tự do của P(x) là 0
`a)`
`@P(x)=x^5-2x^2+7x^4-9x^3-x+2x^2-5x^4`
`P(x)=x^5+(7x^4-5x^4)-9x^3-(2x^2-2x^2)-x`
`P(x)=x^5+2x^4-9x^3-x`
`@Q(x)=5x^4-x^5+4x^2-6+9x^3-8+x^5`
`Q(x)=(-x^5+x^5)+5x^4+9x^3+4x^2-(6+8)`
`Q(x)=5x^4+9x^3+4x^2-14`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`b)` Đa thức `P(x)` có:
`@` Hệ số cao nhất: `1`
`@` Hệ số tự do: `0`
Cho hai đa thức A(x) = 3(x2+2-4x)-2x(x-2)+17 và B(x) = 3x2-7x+3-3(x2-2x+4) a) Thu gọn A(x),B(x). Sắp xếp các đa thức theo luỹ thừa giảm dần của biến. Tìm hệ số cai nhất, hệ số tự do của hai đa thức đó b) Tìm N(x) sao cho N(x)-B(x)=A(x) và M(x) sao cho A(x)-M(x)=B(x).
`@` `\text {Ans}`
`\downarrow`
`a)`
`A(x) = \(3(x^2+2-4x)-2x(x-2)+17\)
`= 3x^2 + 6 - 12x - 2x^2 + 4x + 17`
`= x^2 - 8x + 23`
Hệ số cao nhất: `1`
Hệ số tự do: `23`
`B(x) = \(3x^2-7x+3-3(x^2-2x+4)\)
`=3x^2 - 7x + 3 - 3x^2 + 6x - 12`
`= -x - 9`
Hệ số cao nhất: `-1`
Hệ số tự do: `-9`
`b)`
`N(x) - B(x) = A(x)`
`=> N(x) = A(x) + B(x)`
`=> N(x) = (x^2 - 8x + 23)+(-x-9)`
`= x^2 - 8x + 23 - x - 9`
`= x^2 - 9x + 14`
`A(x) - M(x) = B(x)`
`=> M(x) = A(x) - B(x)`
`=> M(x) = (x^2 - 8x + 23) - (-x - 9)`
`= x^2 - 8x + 23 + x+9`
`= x^2 - 7x +32`
a)A(x) = 3(x^2 + 2 - 4x) - 2x(x - 2) + 17
= 3x^2 + 6 - 12x - 2x^2 + 4x + 17
= x^2 - 2x + 23
b)B(x) = 3x^2 - 7x + 3 - 3(x^2 - 2x + 4)
= 3x^2 - 7x + 3 - 3x^2 + 6x - 12
= -x + -9
A(x) = x^2 - 2x + 23
B(x) = -x - 9
Hệ số cao nhất của đa thức A(x) là 1, hệ số tự do của A(x) là 23.
Hệ số cao nhất của đa thức B(x) là -1, hệ số tự do của B(x) là -9.
b)
N(x) - B(x) = A(x)
N(x) - (-x - 9) = x^2 - 2x + 23
N(x) + x + 9 = x^2 - 2x + 23
N(x) = x^2 - 3x + 14
Vậy, N(x) = x^2 - 3x + 14.
A(x) - M(x) = B(x)
x^2 - 2x + 23 - M(x) = -x - 9
x^2 - 2x + x + 9 + 23 = M(x)
x^2 - x + 32 = M(x)
Vậy, M(x) = x^2 - x + 32.
a: A(x)=3x^2+6-12x-2x^2+4x+17
=x^2-8x+23
B(x)=3x^2-7x+3-3x^2+6x-12=-x-9
Hệ số cao nhất của A(x) là 1
Hệ số tự do của A(x) là 23
Hệ số cao nhất của B(x) là -1
Hệ số tự do của B(x) là -9
b: N(x)=A(x)+B(x)
=x^2-8x+23-x-9
=x^2-9x+14
M(x)=A(x)-B(x)
=x^2-8x+23+x+9
=x^2-7x+32
a) thu gọn đa thức p(x) = 2 x3 - 9x2 + 5 - 2x2- 4x3+7x và sắp xếp theo luỹ thừa giảm dần của biến tìm bậc tìm hệ số tự do
b) cho đa thức p(x) = x4-x3-x-2 tính p (-1)
a) Thu gọn và sắp xếp:
\(P\left(x\right)=2x^3-9x^2+5-4x^3+7x\)
\(P\left(x\right)=\left(2x^3-4x^3\right)-\left(9x^2+2x^2\right)+7x+5\)
\(P\left(x\right)=-2x^3-11x^2+7x+5\)
b) Thay x=1 vào đa thức P(x) ta được:
\(P\left(x\right)=\left(-1\right)^4-\left(-1\right)^3-\left(-1\right)-2=1\)
Sắp xếp đa thức theo lũy thừa giảm dần của biến rồi làm phép chia: (x3 – 7x + 3 – x2) : (x – 3)
x3 – 7x + 3 – x2 = x3 – x2 – 7x + 3
Thực hiện phép chia:
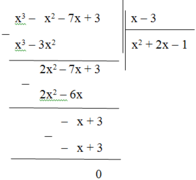
Vậy (x3 – x2 – 7x + 3) : (x – 3) = x2 + 2x – 1
Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi làm phép chia: x 3 - 7 x + 3 - x 2 : ( x - 3 ) .
Bài 4: Cho hai đa thức:
P(x)= \(x^5-2x^2+7x^4-9x^3-x+2x^2-5x^4\)
Q(x)= \(5x^4-x^5+4x^2-6+9x^3-8+x^5\)
a) Sắp xếp các hạng tử của mỗi đa thức trên theo luỹ thừa giảm dần của biến
b) Tìm hệ số cao nhất và hệ số tự do của đa thức P(x)
c)Tính M(x)=P(x)+Q(x)
d)Tính M(2), M(-2),M(\(\dfrac{1}{2}\))
Các bạn chỉ giải phần D thôi nha còn những bạn muốn giải hết thì cũng không sao
a)\(P\left(x\right)=x^5+2x^4-9x^3-x\)
\(Q\left(x\right)=5x^4+9x^3+4x^2-14\)
b) Sửa Tìm hệ số cao nhất và hệ số tự do của đa thức Q(x)
hệ số cao nhất :9
hệ số tự do :- 14
c)\(M\left(x\right)=P\left(x\right)+Q\left(x\right)\)
\(\Leftrightarrow M\left(x\right)=x^5+2x^4-9x^3-x+5x^4+9x^3+4x^2-14\)
\(M\left(x\right)=x^5+6x^4-x-14\)
d)\(M\left(2\right)=2^5+6.2^4-2-14=32-96-2-14=-80\)
\(M\left(-2\right)=\left(-2\right)^5+6.\left(-2\right)^4+2-14=-32-96+2-14=-140\)
\(M\left(\dfrac{1}{2}\right)=\left(\dfrac{1}{2}\right)^5+6.\left(\dfrac{1}{2}\right)^4-\dfrac{1}{2}-14=\dfrac{1}{32}+\dfrac{3}{8}-\dfrac{1}{2}-14=-\dfrac{475}{32}\)
Bài 2
Cho đa thức P(x)=x6+3-x-2x2-x5
a) Sắp xếp các hạng tử của P(x) theo luỹ thừa giảm dần của biến x?
b) Tính giá trị của P(x) khi x=2
c) Tìm nghiệm của đa thức P(x)?
a) \(P\left(x\right)=x^6-x^5-2x^2-x+3\)
b) Thay x = 2 ta có:
\(P\left(2\right)=2^6-2^5-2.2^2-2+3=64-32-8-2+3=25\)
cho hai đa thức P(x)=x^2-5x-3x^5-7x^3+2
Q(x)=x^3-6x-x^2-4x^5-x^4
a)Sắp xếp các hảng tử của mỗi đa thức trên theo luỹ thừa tăng dần của biến
b)Tìm bậc của đa thức.c)Tính P(x)+Q(x) và P(x)-Q(x) d)Tính Q(-1)
a. P(x) = -3x5 - 7x3 + x2 - 5x + 2
Q(x) = -4x5 - x4 + x3 - x2 - 6x
b. Đa thức P(x) và Q(x) có bậc là 5
d. Q(-1) = -4(-1)5 - (-1)4 + (-1)3 - (-1)2 - 6(-1)
= -4.(-1) + 1 + 1 - 1 + 1 - 6.(-1)
= 12
a) Ta có: \(P\left(x\right)=x^2-5x-3x^5-7x^3+2\)
\(=-3x^5-7x^3+x^2-5x+2\)
Ta có: \(Q\left(x\right)=x^3-6x-x^2-4x^5-x^4\)
\(=-4x^5-x^4+x^3-x^2-6x\)
b) Bậc của đa thức P(x) là 5
Bậc của đa thức Q(x) là 5